Theorem of Perpendicular Lines to a Line in Space

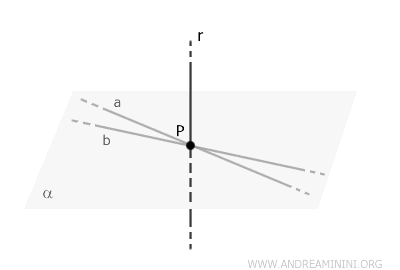
In space, all lines perpendicular to a line $ r $ that pass through a point $ P \in r $ lie within a single plane, $ \alpha $.
contradiction hypothesis

Proof

To demonstrate that all lines perpendicular to $ r $ passing through $ P $ lie in the same plane, I’ll use a proof by contradiction, which will lead to an inconsistency.

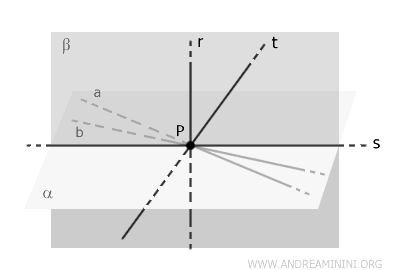
Let’s consider two lines, $ a $ and $ b $, both perpendicular to $ r $ and passing through $ P $.

two lines define a plane perpendicular to line r

These lines define a plane, which I’ll refer to as $ \alpha $, and this plane is also perpendicular to line $ r $. Therefore, $ \alpha $ contains both $ a $ and $ b $.

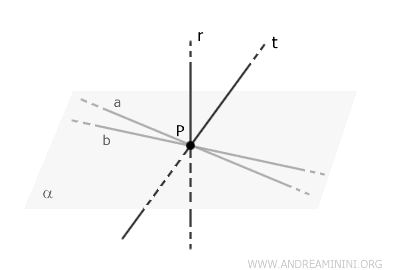
Now, assume for the sake of contradiction that there exists another line $ t $, perpendicular to $ r $ and passing through $ P $, which does not lie in plane $ \alpha $.

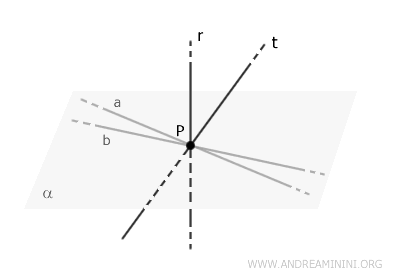
contradiction hypothesis

If line $ t $ does not lie in plane $ \alpha $, then there must exist a different plane, $ \beta $, defined by lines $ t $ and $ r $.

Thus, $ \beta $ is the plane containing both $ r $ and $ t $.

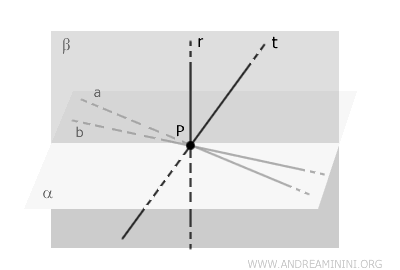
the plane beta

The planes $ \alpha $ and $ \beta $ intersect along a line $ s $, which passes through point $ P $, since both planes contain $ P $.

example

However, this leads to a contradiction.

The line $ s $, as the intersection of planes $ \alpha $ and $ \beta $, belongs to both planes.

Since line $ s $ lies in plane $ \alpha $, which is defined by two lines $ a $ and $ b $ that are perpendicular to $ r $, the theorem of perpendicularity implies that $ s $ is also perpendicular to $ r $.

Now, in plane $ \beta $, there are two lines ($ t $ (by assumption) and $ s $ (by construction)) that are perpendicular to $ r $ and pass through $ P $. But this is impossible, as a line in a single plane can have only one perpendicular passing through a given point.

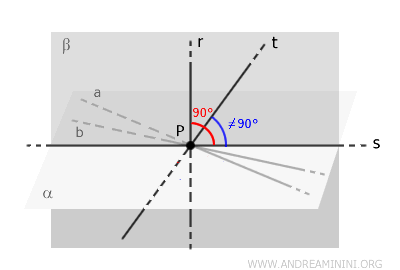
proof

Therefore, within plane $ \beta $, which also contains line $ r $, it is not possible to have two lines perpendicular to $ r $ passing through point $ P $.

Since the assumption that line $ t $ does not lie in plane $ \alpha $ results in a contradiction, we must conclude the opposite: $ t $ must lie in plane $ \alpha $.

This proves that all lines perpendicular to $ r $ and passing through a point $ P $ on $ r $ lie within the same plane, $ \alpha $.

And with that, the theorem is proven.

And so on.