Perpendicular Lines Theorem

If two lines \( r \) and \( s \) are perpendicular to the same plane \( \alpha \), then the two lines are parallel to each other, \( r \parallel s \).

The Proof

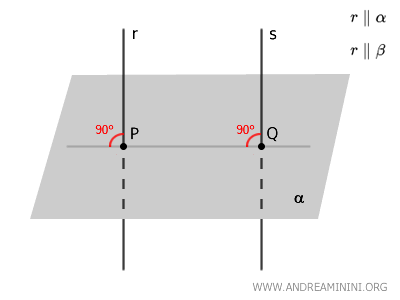
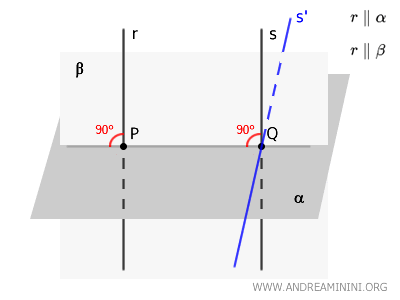
Let us consider two lines \( r \) and \( s \) that are perpendicular to the plane \( \alpha \).

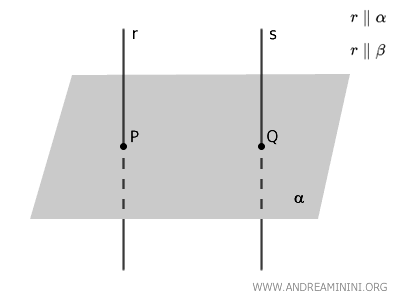
The points \( P \) and \( Q \) are the feet of the perpendiculars drawn from \( r \) and \( s \) onto the plane \( \alpha \).

$$ r \perp \alpha $$

$$ s \perp \alpha $$

By definition, any line perpendicular to a plane forms a right angle (\(90^\circ\)) with all lines lying within that plane.

Thus, the lines \( r \) and \( s \) must form right angles with the line \( PQ \), which lies on plane \( \alpha \) and connects the points \( P \) and \( Q \), the feet of the perpendiculars.

Next, we use lines \( r \) and \( PQ \) to define a new plane, \( \beta \).

By construction, \( r \) and \( PQ \) lie in the same plane \( \beta \).

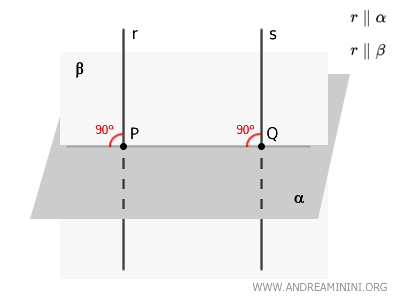
Now, let us assume for the sake of contradiction that \( r \) and \( s \) are not parallel and explore the implications.

If they are not parallel, then either they intersect at some point, or they form an angle other than \(90^\circ\) with each other.

In both cases, this leads to a contradiction:

• If \( r \) and \( s \) intersect in plane \( \beta \), then at least one of them must form an angle other than \(90^\circ\) with line \( PQ \). This contradicts the fact that \( r \) and \( s \) are perpendicular to every line in plane \( \alpha \), including \( PQ \).
  
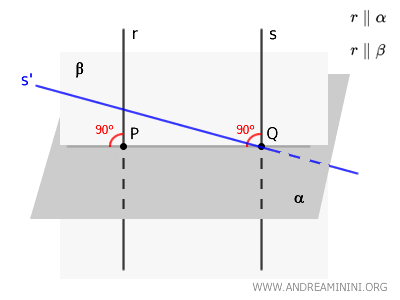
• If \( r \) and \( s \) neither intersect in \( \beta \) nor are parallel, they are skew lines. In this scenario, at least one of them must form an angle other than \(90^\circ\) with the plane \( \alpha \), which contradicts the initial assumption that both \( r \) and \( s \) are perpendicular to \( \alpha \).
  

Therefore, the assumption that \( r \) and \( s \) are not parallel is false, as it leads to a contradiction.

It follows that \( r \) and \( s \) must be parallel.

Additional Notes

Here are some observations and additional insights related to the theorem:

• Theorem of Lines Perpendicular to Another Line in Space
  In three-dimensional space (3D), the theorem stating that two lines perpendicular to the same line are parallel does not hold. This principle applies only in two-dimensional (2D) geometry, where constraints are more restrictive.
  
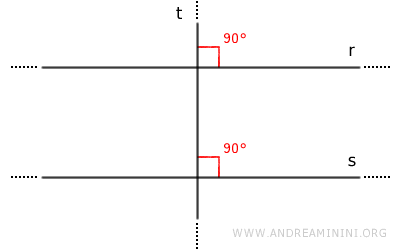
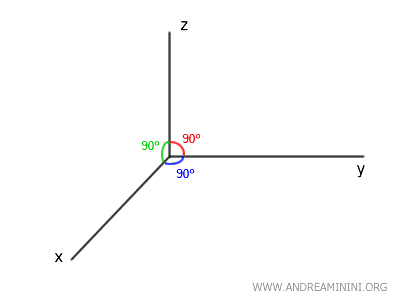
  Why does this theorem hold in a plane but not in 3D space? In a 2D plane, two lines perpendicular to the same line must be parallel because there is no other direction for the lines to "deviate." Perpendicularity to the same line ensures that the two lines lie on parallel paths. However, in 3D space, two lines perpendicular to the same line can belong to different planes, making them not parallel. This is due to the greater freedom of orientation in 3D space, where a line can tilt in multiple directions while remaining perpendicular to the same reference line.

  Example: In a three-dimensional Cartesian coordinate system, the Cartesian axes (\(x\)-\(y\)-\(z\)) are mutually perpendicular, forming right angles (\(90^\circ\)):
  - The \(x\)-axis is perpendicular to both the \(y\)-axis and the \(z\)-axis.
  - The \(y\)-axis is perpendicular to both the \(x\)-axis and the \(z\)-axis.
  - The \(z\)-axis is perpendicular to both the \(x\)-axis and the \(y\)-axis.
  However, none of these axes (\(x, y, z\)) are parallel because each belongs to a different plane (\(xy\), \(xz\), \(yz\)).
  

And so on.