Perpendicular Line to a Plane Theorem

Given a plane \( \alpha \) and a point \( P \), there is exactly one line \( r \) that passes through \( P \) and is perpendicular to the plane \( \alpha \).

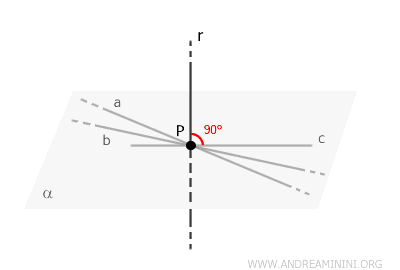
Every plane in space has a unique perpendicular direction, defined by its normal vector.

The line \( r \) passes through point \( P \) and aligns with the direction of the normal vector to the plane \( \alpha \).

Note: The uniqueness of this line stems from the fact that the normal vector is unique (apart from scalar multiples), meaning there is only one line with this property.

Proof

Let us examine the plane \( \alpha \) and select an arbitrary point \( P \) on it.

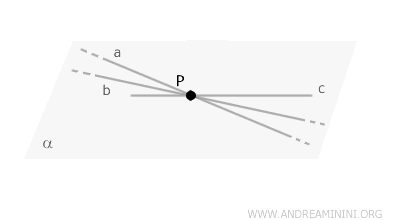
A plane contains infinitely many points and an infinite number of coplanar lines \( a \), \( b \), \( c \), and so on.

By definition, a line is perpendicular to the plane \( \alpha \) if it forms a right angle with every line passing through \( P \) and lying within the plane \( \alpha \).

Therefore, given point \( P \), we can always define a perpendicular line \( r \) starting at \( P \) that forms right angles with all lines in the plane \( \alpha \).

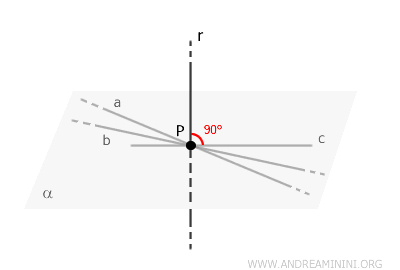
Now, we need to prove that this perpendicular line \( r \) is unique, meaning no other line shares this property.

Assume, for the sake of contradiction, that there are two distinct lines \( r \) and \( r' \) passing through \( P \) and perpendicular to the plane \( \alpha \).

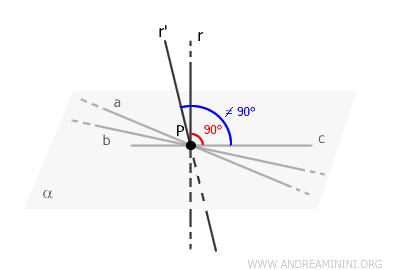
If this were true, at least one of the lines, \( r \) or \( r' \), would fail to form a \( 90^\circ \) angle with some lines in the plane. Otherwise, \( r \) and \( r' \) would coincide, contradicting the assumption that they are distinct.

This contradiction shows that \( r \) and \( r' \) cannot both exist as separate entities; they must be the same line.

Thus, there is exactly one line that passes through \( P \) and is perpendicular to the plane \( \alpha \).

And so the theorem is proven.