Coplanar Lines

Two or more lines are called coplanar lines if they lie on the same plane.

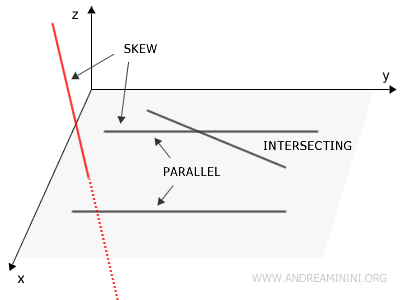
In other words, two or more lines are coplanar if a single plane contains them all.

Coplanar lines can be:

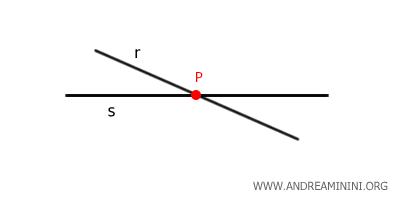
• Intersecting Lines
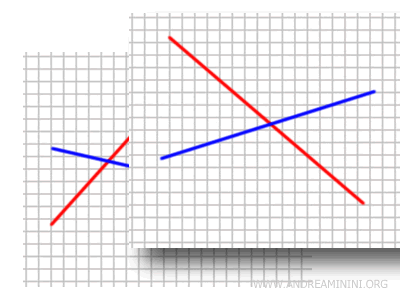
  Two lines in a plane are intersecting if they meet at a point. Mathematically, this means there is a point in space (x, y, z) that belongs to both lines.
  
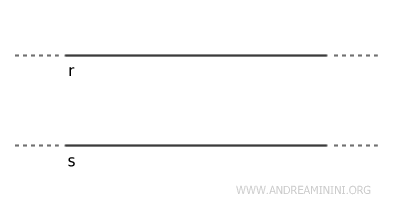
• Parallel Lines
  Two or more lines in a plane are parallel if they do not intersect at any point. They have the same direction but never meet, and they lie in the same plane.
  
• Coincident Lines
  Two lines are coincident if they share all points. Since a line consists of an infinite number of points, coincident lines have all points in common. This is a special case of parallel lines. These lines are essentially the same line, even if they are represented by different equations.

The Difference Between Coplanar Lines and Skew Lines. Coplanar lines differ from skew lines because the latter are neither parallel nor intersecting. Hence, skew lines do not lie entirely on the same plane. Additionally, skew lines are a feature of three-dimensional space and cannot exist in a two-dimensional plane. In contrast, coplanar lines are a fundamental concept in Euclidean geometry.

A Practical Example

A common example of coplanar lines is lines drawn on a sheet of paper.

All lines drawn on the same sheet of paper are coplanar because they lie on the same plane, which is the surface of the paper. They can be parallel or intersecting.

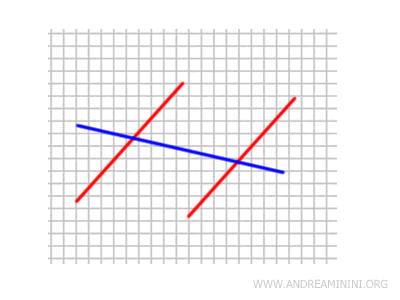
Conversely, two lines drawn on two different sheets of paper placed one on top of the other (e.g., in a notebook) are not coplanar.

And so on.