Skew Lines

Skew lines are two lines in a three-dimensional space (x, y, z) that do not lie on the same plane, are not parallel, and do not intersect.

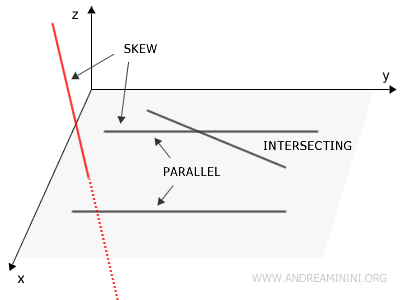
In other words, there is no single plane that can contain both skew lines.

This means that skew lines have no points in common, even if they intersect the same plane. Additionally, they are not parallel to each other.

The concept of skew lines is typical of three-dimensional geometry (x, y, z), because in a two-dimensional space (x, y), two lines must lie on the same plane, and thus either intersect or are parallel. Unlike lines in a two-dimensional space, which either intersect or are parallel, skew lines never meet.

A Practical Example

Consider a solid in three-dimensional space.

For example, a cube.

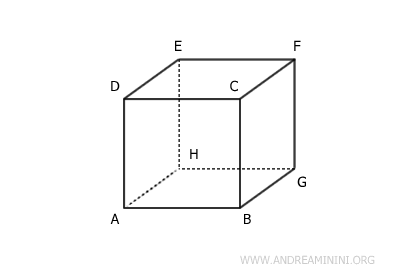
Now imagine a line r (red) passing through the vertices E and F of the cube and a line s (blue) passing through the vertices A and H of the cube.

The lines r and s, which pass through the edges EF and AH of the cube, are skew lines because they do not lie on the same plane, do not intersect, and are not parallel.

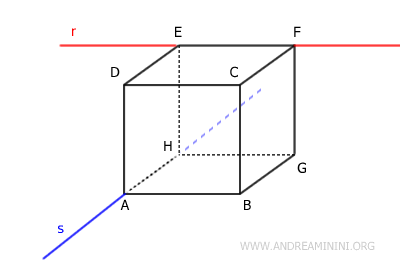
Conversely, the lines r (red) and t (green) are not skew lines because, although they do not lie on the same plane and do not intersect, they are parallel.

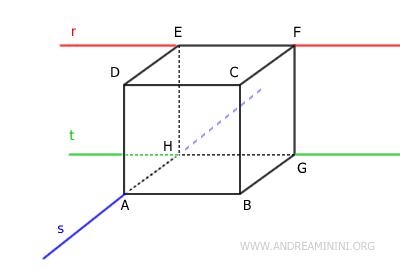
Lines r (red) and p (purple) are also not skew because they intersect at point E.

Similarly, lines s (blue) and t (green) are not skew because they intersect at point H and lie on the same plane.

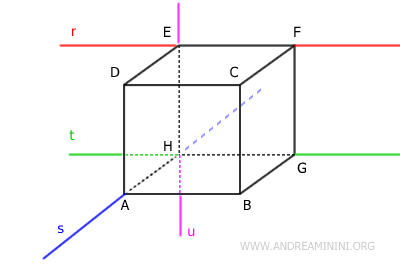
Finally, lines s (blue) and q (yellow) are skew lines because they do not intersect and are not parallel.

For the same reason, lines r (red) and q (yellow) and lines t (green) and q (yellow) are also skew lines.

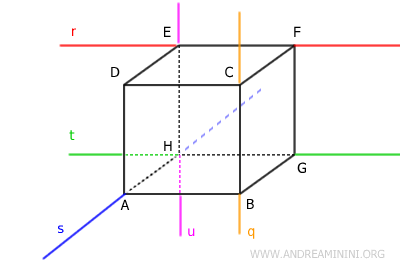
Conversely, lines u (purple) and q (yellow) are not skew because they are parallel and can be contained in the same plane.

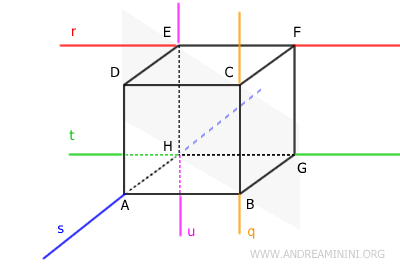
From these examples, we can deduce the main characteristics of skew lines: they must never intersect and must not be parallel.

Note: These two characteristics (non-intersection and non-parallelism) are sufficient to define skew lines, as they indirectly imply that the two lines do not lie entirely on the same plane.

Characteristics of Skew Lines

Lines are skew if they meet the following characteristics:

• Non-intersection
  Skew lines never meet. Therefore, they do not intersect and have no points in common.
• Non-parallelism
  Even though skew lines do not intersect, they are not parallel to each other.

In other words, skew lines are distinguished by not intersecting and not being parallel.

This means that they do not lie entirely on the same plane. In fact, in a plane, two lines can only be either parallel or intersecting.

However, this does not exclude the possibility that skew lines may have points lying on the same plane, as long as they are different points.

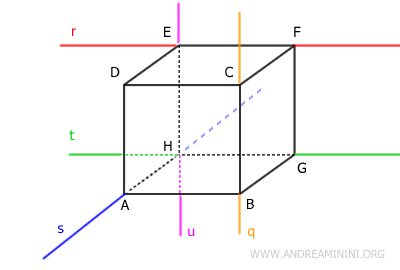
For example, lines r (blue) and q (yellow) are skew lines even though they have points A and B on the same plane. However, the two points are not coincident.

Why Can’t Skew Lines Intersect?

Skew lines cannot share a common point because, by definition, they exist in different planes.

To demonstrate this, let’s assume for the sake of contradiction that two skew lines, r₁ and r₂, intersect at a point \( P \).

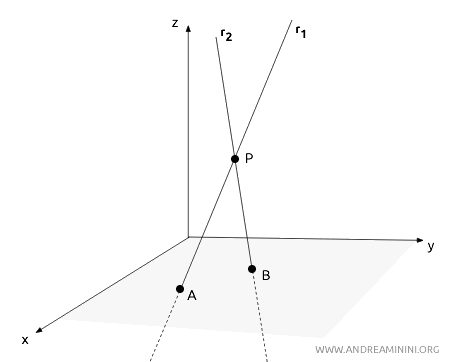
If this were true, we could identify another point \( A \) on one line and a point \( B \) on the other, both distinct from \( P \).

The three points \( P \), \( A \), and \( B \) would define a single plane β that contains both lines, making them coplanar.

But this would contradict the very definition of skew lines, which are always non-coplanar.

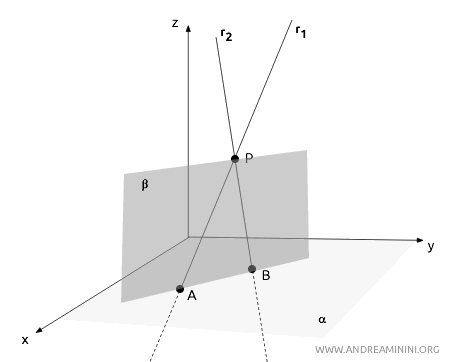
Therefore, if two lines share a point, they must lie in the same plane and cannot be skew.

In conclusion, skew lines and intersecting lines are fundamentally incompatible: if two lines are coplanar, they cannot be skew; if they are skew, they cannot intersect.

And so on.