Equation of a Hyperbola Given an Asymptote and a Vertex
To find the equation of a hyperbola centered at the origin, given an asymptote and a vertex $ A(a;0) $ or $ B(0;b) $, follow these steps:
- Determine whether the transverse axis is horizontal or vertical based on the information provided. This will help you write the correct equation for the hyperbola. If it's unclear, consider both possibilities: $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 $$
- Write the equation of the asymptote $$ y = \pm \frac{b}{a} x $$ and substitute the known semi-axis length ($ a $ or $ b $).
- Solve the resulting system of equations to find the missing semi-axis.
Once you have the values for $ a $ and $ b $, you can complete the hyperbola’s equation.
A Practical Example
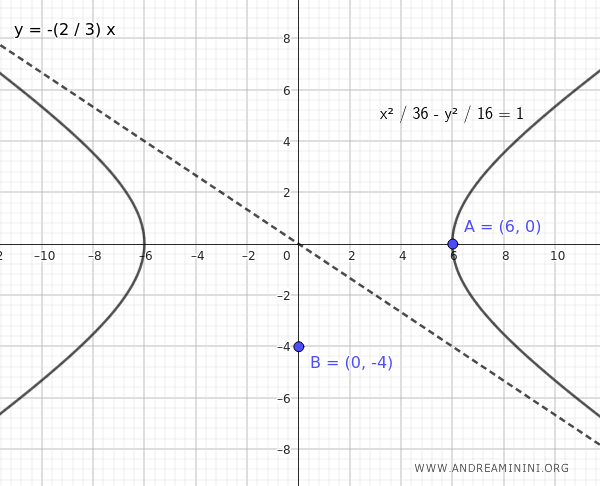
Let's consider a hyperbola with a real vertex at $ A(6;0) $ and an asymptote given by the equation $ y = - \frac{2}{3} x $.
Since the vertex $ A(6;0) $ is specified as "real," it lies on the transverse axis, which also contains the foci.
This means the transverse axis is the x-axis, and the corresponding hyperbola equation is:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
Now, set up a system of equations using the asymptote and the hyperbola equation:
$$ \begin{cases} y = \frac{b}{a} x \\ \\ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \end{cases} $$
The vertex $ A(6;0) $ is located on the x-axis, $ a=6 $ units from the center of the hyperbola.
Substituting $ a = 6 $ gives us:
$$ \begin{cases} y = \frac{b}{6} x \\ \\ \frac{x^2}{6^2} - \frac{y^2}{b^2} = 1 \end{cases} $$
Which simplifies to:
$$ \begin{cases} y = \frac{b}{6} x \\ \\ \frac{x^2}{36} - \frac{y^2}{b^2} = 1 \end{cases} $$
We know the asymptote of the hyperbola is $ y = - \frac{2}{3} x $.
So, we set up the system:
$$ \begin{cases} - \frac{2}{3} x = \frac{b}{6} x \\ \\ \frac{x^2}{36} - \frac{y^2}{b^2} = 1 \end{cases} $$
Divide both sides of the first equation by $ x $ and simplify:
$$ \begin{cases} - \frac{2}{3} = \frac{b}{6} \\ \\ \frac{x^2}{36} - \frac{y^2}{b^2} = 1 \end{cases} $$
Now, solve for $ b $ in the first equation:
$$ \begin{cases} b = - \frac{2}{3} \cdot 6 \\ \\ \frac{x^2}{36} - \frac{y^2}{b^2} = 1 \end{cases} $$
Which simplifies to:
$$ \begin{cases} b = -4 \\ \\ \frac{x^2}{36} - \frac{y^2}{b^2} = 1 \end{cases} $$
Substitute $ b = -4 $ into the second equation:
$$ \begin{cases} y = \frac{b}{6} x \\ \\ \frac{x^2}{36} - \frac{y^2}{(-4)^2} = 1 \end{cases} $$
Which simplifies further to:
$$ \begin{cases} y = \frac{b}{6} x \\ \\ \frac{x^2}{36} - \frac{y^2}{16} = 1 \end{cases} $$
Therefore, the equation of the hyperbola is:
$$ \frac{x^2}{36} - \frac{y^2}{16} = 1 $$
This is the equation for the hyperbola with a real vertex at $ A(6;0) $ and an asymptote given by $ y = - \frac{2}{3} x $.
And so on.
