Tangent Lines to the Hyperbola

To find the tangent lines to a hyperbola that pass through a point P(x₀, y₀), we create a system using the hyperbola's equation and the equation of the family of lines passing through point P.

$$ \begin{cases} \frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 \\ \\ y-y_0 = m (x-x_0) \end{cases} $$

This system allows us to find a quadratic equation in the variable y.

To determine the tangent lines, we impose the tangency condition $ \Delta = 0 $ on the quadratic equation and solve for the slope m.

If the equation has two distinct real solutions m₁≠m₂, there are two tangent lines to the hyperbola passing through the point P(x₀, y₀), indicating that this point is outside the hyperbola.
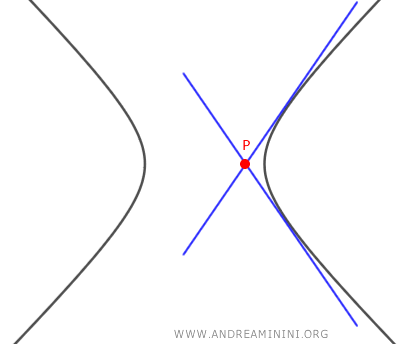
If the equation has a single real solution m₁=m₂, there is one tangent line to the hyperbola passing through the point P(x₀, y₀), indicating that this point lies on the hyperbola.
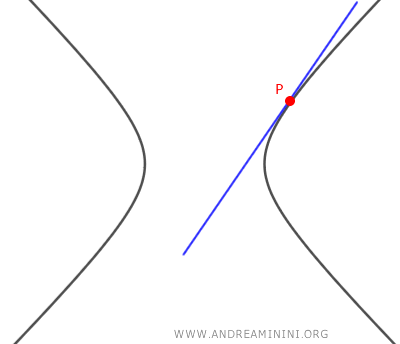
If the equation has no real solutions, there are no tangent lines to the hyperbola passing through the point P(x₀, y₀).

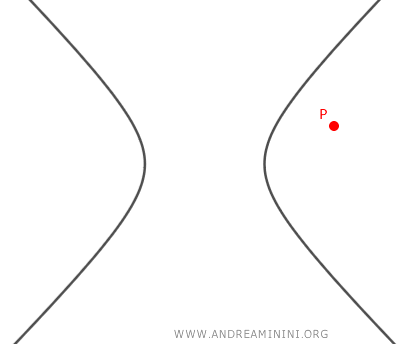
Practical Example

Consider the equation

$$ \frac{x^2}{16} - \frac{y^2}{16} = 1 $$

We need to find the tangent line(s) passing through the point $ P\left( \frac{16}{5}, 0 \right) $.

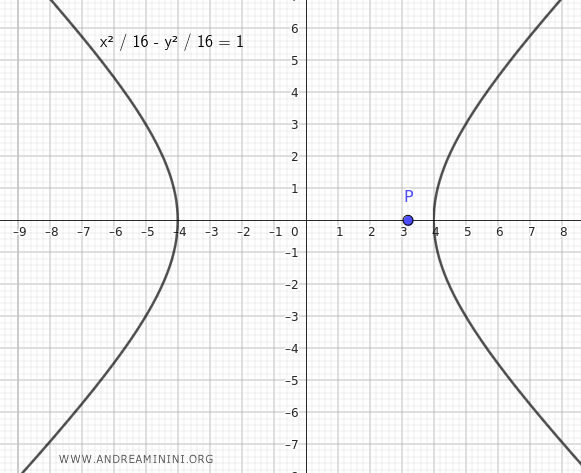
Example

First, we write a system with the equation of the hyperbola and the equation of the family of lines passing through $ P\left( \frac{16}{5}, 0 \right) $.

$$ \begin{cases} \frac{x^2}{16} - \frac{y^2}{16} = 1 \\ \\ (y-y_0)=m(x-x_0) \end{cases} $$

In this case, the coordinates of the point are $ x_0 = \frac{16}{5} $ and $ y_0 = 0 $.

$$ \begin{cases} \frac{x^2}{16} - \frac{y^2}{16} = 1 \\ \\ (y-0)=m(x-\frac{16}{5}) \end{cases} $$

$$ \begin{cases} \frac{x^2}{16} - \frac{y^2}{16} = 1 \\ \\ y=mx-\frac{16m}{5} \end{cases} $$

Next, we solve for the variable y in both equations:

$$ \begin{cases} y^2 = 16 \left( \frac{x^2}{16} -1 \right) \\ \\ y=mx-\frac{16m}{5} \end{cases} $$

$$ \begin{cases} y^2 = x^2 - 16 \\ \\ y=mx-\frac{16m}{5} \end{cases} $$

$$ \begin{cases} y = \sqrt{ x^2 - 16 } \\ \\ y=mx-\frac{16m}{5} \end{cases} $$

The resulting equation is:

$$ \sqrt{ x^2 - 16 } = mx-\frac{16m}{5} $$

$$ \left( \sqrt{ x^2 - 16 } \right)^2 = \left( mx-\frac{16m}{5} \right)^2 $$

$$ x^2 - 16 = m^2x^2 - 2 \cdot mx \cdot \frac{16m}{5} + \left( \frac{16m}{5} \right)^2 $$

$$ x^2 - 16 = m^2x^2 - \frac{32m^2x}{5} + \frac{256m^2}{25} $$

$$ x^2 - 16 - m^2x^2 + \frac{32m^2x}{5} - \frac{256m^2}{25} = 0 $$

$$ x^2 (1- m^2 ) + x \left( \frac{32m^2}{5} \right) - 16 - \frac{256m^2}{25} = 0 $$

This is a quadratic equation in x.

We apply the tangency condition $ \Delta = 0 $.

$$ \Delta = b^2 - 4ac = 0 $$

In this case, $ a =1- m^2 $, $ b = \frac{32m^2}{5} $, and $ c = - 16 - \frac{256m^2}{25} $.

$$ \left( \frac{32m^2}{5} \right)^2 - 4 \cdot (1-m^2) \cdot \left( - 16 - \frac{256m^2}{25} \right) = 0 $$

$$ \frac{1024m^4}{25} - \left(4-4m^2\right) \cdot \left( - 16 - \frac{256m^2}{25} \right) = 0 $$

$$ \frac{1024m^4}{25} - 4 \cdot \left( - 16 - \frac{256m^2}{25} \right) + 4m^2 \cdot \left( - 16 - \frac{256m^2}{25} \right) = 0 $$

$$ \require{cancel} \cancel{ \frac{1024m^4}{25} } + 64 + \frac{1024m^2}{25} - 64m^2 - \cancel{ \frac{1024m^4}{25} } = 0 $$

$$ \frac{1024m^2-1600m^2}{25} + 64 = 0 $$

$$ - \frac{576m^2}{25} = -64 $$

$$ m^2 = \frac{64 \cdot 25}{576} $$

$$ m^2 = \frac{1600}{576} $$

$$ m^2 = \frac{800}{288} $$

$$ m^2 = \frac{400}{144} $$

$$ m^2 = \frac{200}{72} $$

$$ m^2 = \frac{100}{36} $$

$$ m^2 = \frac{25}{9} $$

$$ \sqrt{ m^2 } = \sqrt{ \frac{25}{9} } $$

$$ m = \pm \frac{5}{3} $$

Once the slope is found, we substitute it back into the equation of the family of lines:

$$ y=mx-\frac{16m}{5} $$

We need to consider both values of the slope:

For $ m = \frac{5}{3} $ $$ y = \frac{5}{3} x - \frac{16 \cdot \frac{5}{3}}{5} $$ $$ y = \frac{5}{3} x - \frac{16 \cdot \frac{5}{3}}{5} $$ $$ y = \frac {5}{3} x - \frac{80}{15} $$ $$ y = \frac{5}{3} x - \frac{16}{3} $$ $$ y - \frac{5}{3} x + \frac{16}{3} = 0 $$ $$ 3 \cdot \left( y - \frac{5}{3} x + \frac{16}{3} \right) = 3 \cdot 0 $$ $$ 3y - 5x + 16 = 0 $$
For $ m = - \frac{5}{3} $ $$ y = - \frac{5}{3} x - \frac{16 \cdot \left( - \frac{5}{3} \right)}{5} $$ $$ y = - \frac{5}{3} x + \frac{80}{15} $$ $$ y = - \frac{5}{3} x + \frac{16}{3} $$ $$ y + \frac{5}{3} x - \frac{16}{3} = 0 $$ $$ 3 \cdot \left( y + \frac{5}{3} x - \frac{16}{3} \right) = 3 \cdot 0 $$ $$ 3y + 5x - 16 = 0 $$

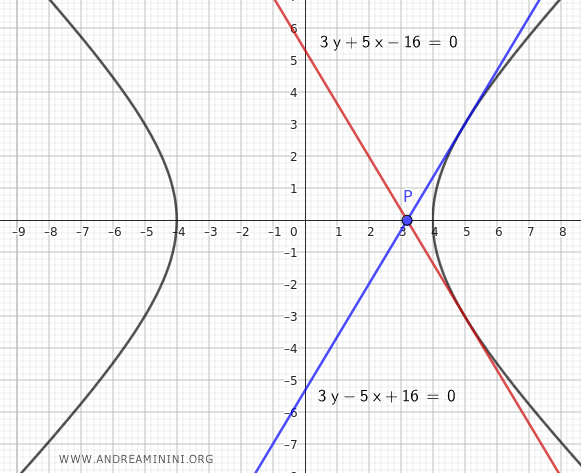
Here is the graph of the tangent lines to the hyperbola passing through the point $ P\left( \frac{16}{5}, 0 \right) $.

Graph

And so on.