Hyperbolas Centered at a Point (p,q)

The equation of a hyperbola centered at a point \((p, q)\) is derived by shifting the canonical hyperbola, which is originally centered at the origin \((0, 0)\).

• Hyperbola with the transverse axis along the \(x\)-axis:
  The standard equation of a hyperbola centered at the origin, with the transverse axis along the \(x\)-axis, is: $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ If the center of the hyperbola is moved from \((0, 0)\) to \((p, q)\), the equation becomes: $$
  \frac{(x-p)^2}{a^2} - \frac{(y-q)^2}{b^2} = 1 $$
• Hyperbola with the transverse axis along the \(y\)-axis:
  The standard equation of a hyperbola centered at the origin, with the transverse axis along the \(y\)-axis, is: $$
  \frac{y^2}{a^2} - \frac{x^2}{b^2} = 1 $$ When the center is shifted to \((p, q)\), the equation becomes: $$
  \frac{(y-q)^2}{a^2} - \frac{(x-p)^2}{b^2} = 1 $$

In both cases, \(a\) represents the distance from the center to the vertices along the transverse axis, while \(b\) is the distance from the center to the endpoints of the conjugate axis (also called the imaginary axis).

The General Equation of a Translated Hyperbola

The general form of a conic section is given by the equation:

$$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $$

In this equation, \(Ax^2\) and \(Cy^2\) are the quadratic terms, \(Bxy\) is the mixed term, and \(Dx\) and \(Ey\) are the linear terms. \(F\) is a constant term.

To transform this general form from the equation of a hyperbola centered at \((p, q)\), such as:

$$ \frac{(x-p)^2}{a^2} - \frac{(y-q)^2}{b^2} = 1 $$

we expand the standard equation by squaring the terms:

$$ \frac{(x-p)^2}{a^2} - \frac{(y-q)^2}{b^2} = 1 $$

$$ \frac{(x^2 - 2px + p^2)}{a^2} - \frac{(y^2 - 2qy + q^2)}{b^2} = 1 $$

Multiplying both sides by \(a^2b^2\) to clear the denominators, we get:

$$ b^2(x^2 - 2px + p^2) - a^2(y^2 - 2qy + q^2) = a^2b^2 $$

Expanding and rearranging all terms to one side gives us:

$$ b^2x^2 - a^2y^2 - 2b^2px + 2a^2qy + (b^2p^2 - a^2q^2 - a^2b^2) = 0 $$

When compared with the general conic form \(Ax^2 + By^2 + Cx + Dy + E = 0\), the coefficients are:

• \(A = b^2\)
• \(B = -a^2\)
• \(C = -2b^2p\)
• \(D = 2a^2q\)
• \(E = b^2p^2 - a^2q^2 - a^2b^2\)

This expanded form represents the equation of a hyperbola that has been translated from the origin. Each term corresponds to a specific component of the general conic equation for a hyperbola not centered at the origin.

A Practical Example

Let’s consider a practical example of a translated hyperbola.

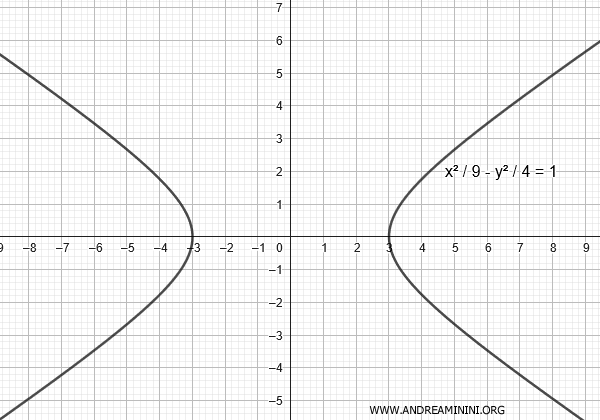
Start with the standard equation of a hyperbola with its transverse axis along the \(x\)-axis (horizontal) and centered at the origin \((0, 0)\):

$$ \frac{x^2}{9} - \frac{y^2}{4} = 1 $$

This describes a horizontal hyperbola where \(a^2 = 9\) (so \(a = 3\)) and \(b^2 = 4\) (so \(b = 2\)).

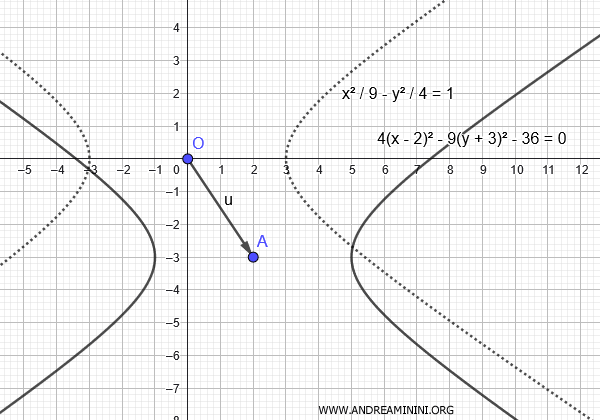
Now, let's translate the center of the hyperbola from \((0, 0)\) to \((p, q) = (2, -3)\).

The equation of the translated hyperbola becomes:

$$ \frac{(x - 2)^2}{9} - \frac{(y + 3)^2}{4} = 1 $$

We can expand this equation to get the general form:

$$ \frac{(x^2 - 4x + 4)}{9} - \frac{(y^2 + 6y + 9)}{4} = 1 $$

Multiplying through by 36 (the least common multiple of 9 and 4) to eliminate the denominators, we get:

$$ 4(x^2 - 4x + 4) - 9(y^2 + 6y + 9) = 36 $$

Expanding and simplifying this gives:

$$ 4x^2 - 16x + 16 - 9y^2 - 54y - 81 = 36 $$

Rearranging all terms to one side, we have:

$$ 4x^2 - 9y^2 - 16x - 54y + 16 - 81 - 36 = 0 $$

Simplifying the constant terms results in:

$$ 4x^2 - 9y^2 - 16x - 54y - 101 = 0 $$

This is the equation of the hyperbola with its center translated to \((2, -3)\), while maintaining the original \(a^2\) and \(b^2\) values.

Finding the Coordinates of the Hyperbola's Center

The coordinates of the center of a hyperbola not centered at the origin, given by the equation $$ Ax^2 + By^2 + Cx + Dy + E = 0 $$, can be found using the formula $$ \left(p, q\right) = \left(-\frac{C}{2A}, - \frac{D}{2B}\right) $$

Example

For a hyperbola not centered at the origin, consider the general equation:

$$ 4x^2 - 9y^2 - 16x - 54y - 101 = 0 $$

Here, \( A=4 \), \( B=-9 \), \(C=-16 \), \(D=-54 \), and \( E=-101 \).

The coordinates of the center are calculated as follows:

$$ \left(p, q\right) = \left(-\frac{C}{2A}, - \frac{D}{2B}\right) $$

$$ \left(p, q\right) = \left(-\frac{-16}{2 \cdot 4}, - \frac{-54}{2 \cdot (-9)}\right) $$

$$ \left(p, q\right) = \left(\frac{16}{8}, - \frac{54}{18}\right) $$

$$ \left(p, q\right) = \left( 2, -3\right) $$

Proof

Let’s take the general form of a hyperbola not centered at the origin:

$$ Ax^2 + By^2 + Cx + Dy + E = 0 $$

We start by grouping the quadratic and linear terms:

$$ (Ax^2 + Cx) + (By^2 + Dy) = -E $$

Next, we complete the square for the \(x\) and \(y\) terms:

• For the \(x\) term:
  Consider the terms involving \(x\), \(Ax^2 + Cx\), and factor out \(A\): $$
  A\left(x^2 + \frac{C}{A}x\right) $$ Complete the square by adding and subtracting \(\left(\frac{C}{2A}\right)^2\): $$
  A\left(x^2 + \frac{C}{A}x + \left(\frac{C}{2A}\right)^2 - \left(\frac{C}{2A}\right)^2\right) = A\left(\left(x + \frac{C}{2A}\right)^2 - \left(\frac{C}{2A}\right)^2\right) $$ Which simplifies to: $$ A\left(x + \frac{C}{2A}\right)^2 - A\left(\frac{C}{2A}\right)^2 $$
• For the \(y\) term:
  Consider the terms involving \(y\), \(By^2 + Dy\), and factor out \(B\): $$ B\left(y^2 + \frac{D}{B}y\right) $$ Complete the square by adding and subtracting \(\left(\frac{D}{2B}\right)^2\): $$ B\left(y^2 + \frac{D}{B}y + \left(\frac{D}{2B}\right)^2 - \left(\frac{D}{2B}\right)^2\right) = B\left(\left(y + \frac{D}{2B}\right)^2 - \left(\frac{D}{2B}\right)^2\right) $$ Which simplifies to: $$ B\left(y +\frac{D}{2B}\right)^2 - B\left(\frac{D}{2B}\right)^2 $$

Substituting the completed squares back into the equation gives:

$$ Ax^2 + Cx + By^2 + Dy = -E $$

$$ (Ax^2 + Cx) + ( By^2 + Dy) = -E $$

$$ A\left(x^2 + \frac{C}{A}x\right) + B\left(y^2 + \frac{D}{B}y\right) = -E $$

$$ A\left(x + \frac{C}{2A}\right)^2 - A\left(\frac{C}{2A}\right)^2 + B\left(y + \frac{D}{2B}\right)^2 - B\left(\frac{D}{2B}\right)^2 = E $$

$$ A\left(x + \frac{C}{2A}\right)^2 + B\left(y + \frac{D}{2B}\right)^2 = E + A\left(\frac{C}{2A}\right)^2 + B\left(\frac{D}{2B}\right)^2 $$

This form clearly shows the translation, indicating that the center of the hyperbola is given by:

$$ \left(-\frac{C}{2A},- \frac{D}{2B}\right) $$

This confirms that the coordinates of the center are:

$$ \left(p, q\right) = \left(-\frac{C}{2A}, - \frac{D}{2B}\right) $$

Axes of Symmetry

The axes of symmetry of a hyperbola not centered at the origin, given by the equation $$ Ax^2 + By^2 + Cx + Dy + E = 0 $$, are defined by the center coordinates \( (p,q) \) and are given by the lines $$ x = p = -\frac{C}{2A} $$ $$ y = q = - \frac{D}{2B} $$

Example

For a hyperbola not centered at the origin, the general equation is:

$$ 4x^2 - 9y^2 - 16x - 54y - 101 = 0 $$

In this case, \( A=4 \), \( B=-9 \), \(C=-16 \), \(D =-54 \), and \( E=-101 \).

The axes of symmetry of the hyperbola are:

$$ x = p = -\frac{C}{2A} = -\frac{-16}{2 \cdot 4} = 2 $$

$$ y = q = - \frac{D}{2B} = - \frac{-54}{2 \cdot (-9)} = -3 $$

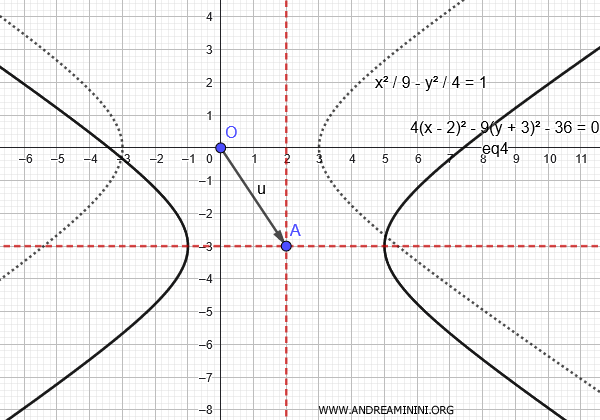
Proof

The axes of symmetry of a hyperbola correspond to the lines that pass through the center and are parallel to the coordinate axes, or at an angle if the hyperbola is rotated.

If the hyperbola is not rotated (i.e., the axes are parallel to the coordinate axes), the equations of the axes of symmetry are:

$$ x = p $$

$$ y = q $$

where \((p, q)\) is the center of the hyperbola.

Note: If the hyperbola is rotated, the equations of the axes of symmetry can be determined by a transformation involving the angle of rotation \(\theta\), which is derived from the coefficients \(A\), \(B\), and any mixed terms (if present) in the general equation. Generally, this requires solving for the direction of the axes of symmetry.

And so forth.