Finding the Equation of a Hyperbola Given a Point and a Focus

To determine the equation of a hyperbola centered at the origin, given a point \( P(x_0, y_0) \) and one of its foci \( F(c, 0) \), you can follow two different methods:

• Set up a system of equations using $ c^2 = a^2 + b^2 $ and the hyperbola equation by substituting $ x $ and $ y $ with the coordinates of point \( P(x_0, y_0) \): $$ \begin{cases} \frac{x_0^2}{a^2} - \frac{y_0^2}{b^2} = 1 \\ \\ c^2 = a^2 + b^2 \end{cases} $$
• Calculate the distance between point P and the foci, knowing that $ | PF - PF' | = 2a $. Once you find the distance $ a $ from a vertex to the center, you can also calculate the distance $ b $ of the other vertex using the relation $ c^2 = a^2 + b^2 $.

Note: If the focus is on the x-axis, the equation of the hyperbola is $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$. Conversely, if the focus is on the y-axis, the equation to consider is $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$.

Method 1

Let's assume we have a hyperbola centered at the origin that passes through the point \( P(3, 4) \) and has its focus at \( F(5, 0) \).

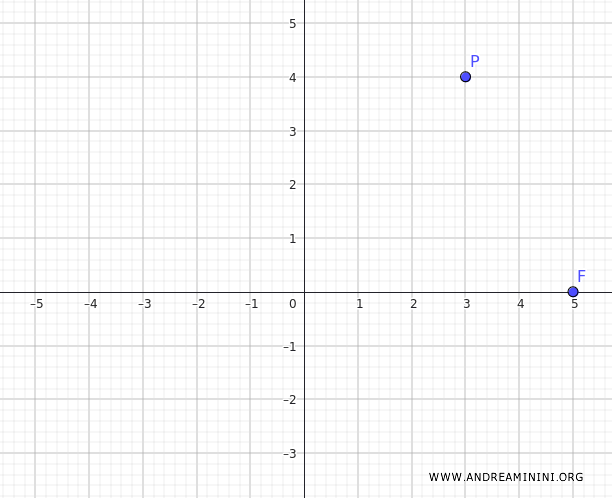
Since the focus is on the x-axis, the standard form of the hyperbola's equation is:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

We set up a system of equations using the standard form of the hyperbola and the relation $ c^2 = a^2 + b^2 $:

$$ \begin{cases} \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \\ \\ c^2 = a^2 + b^2 \end{cases} $$

Substitute \( x \) and \( y \) with the coordinates of the point \( P(3, 4) \), i.e., \( x = 3 \) and \( y = 4 \):

$$ \begin{cases} \frac{3^2}{a^2} - \frac{4^2}{b^2} = 1 \\ \\ c^2 = a^2 + b^2 \end{cases} $$

$$ \begin{cases} \frac{9}{a^2} - \frac{16}{b^2} = 1 \\ \\ c^2 = a^2 + b^2 \end{cases} $$

Since we know the coordinates of the focus \( F(c,0) = (5,0) \), we know that the distance from the focus to the center of the hyperbola is \( c = 5 \):

$$ \begin{cases} \frac{9}{a^2} - \frac{16}{b^2} = 1 \\ \\ 5^2 = a^2 + b^2 \end{cases} $$

$$ \begin{cases} \frac{9}{a^2} - \frac{16}{b^2} = 1 \\ \\ 25 = a^2 + b^2 \end{cases} $$

Next, solve the system using the substitution method.

$$ \begin{cases} \frac{9}{(25 - b^2)} - \frac{16}{b^2} = 1 \\ \\ a^2 = 25 - b^2 \end{cases} $$

$$ \begin{cases} \frac{9b^2 - 16(25 - b^2)}{b^2(25 - b^2)} = 1 \\ \\ a^2 = 25 - b^2 \end{cases} $$

$$ \begin{cases} 9b^2 - 16(25 - b^2) = b^2(25 - b^2) \\ \\ a^2 = 25 - b^2 \end{cases} $$

$$ \begin{cases} 9b^2 - 400 + 16b^2 = 25b^2 - b^4 \\ \\ a^2 = 25 - b^2 \end{cases} $$

$$ \begin{cases} 9b^2 - 400 + 16b^2 - 25b^2 + b^4 = 0 \\ \\ a^2 = 25 - b^2 \end{cases} $$

$$ \begin{cases} b^4 - 400 = 0 \\ \\ a^2 = 25 - b^2 \end{cases} $$

$$ \begin{cases} \sqrt{b^4} = \sqrt{400} \\ \\ a^2 = 25 - b^2 \end{cases} $$

$$ \begin{cases} b^2 = 20 \\ \\ a^2 = 25 - b^2 \end{cases} $$

Note: The square root of 400 is \( \sqrt{400} = \pm 20 \), but since \( b \) represents a length, we discard the negative value (-20) and keep only the positive value (+20).

Once we find \( b^2 = 20 \), we substitute it into the second equation to find the distance of the other vertex from the center, \( a \):

$$ \begin{cases} b^2 = 20 \\ \\ a^2 = 25 - 20 \end{cases} $$

$$ \begin{cases} b^2 = 20 \\ \\ a^2 = 5 \end{cases} $$

Now, we can write the standard equation of the hyperbola by substituting \( a^2 = 5 \) and \( b^2 = 20 \):

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

$$ \frac{x^2}{5} - \frac{y^2}{20} = 1 $$

This is the equation of the hyperbola that passes through the point \( P(3,4) \) and has a focus at \( F(5,0) \).

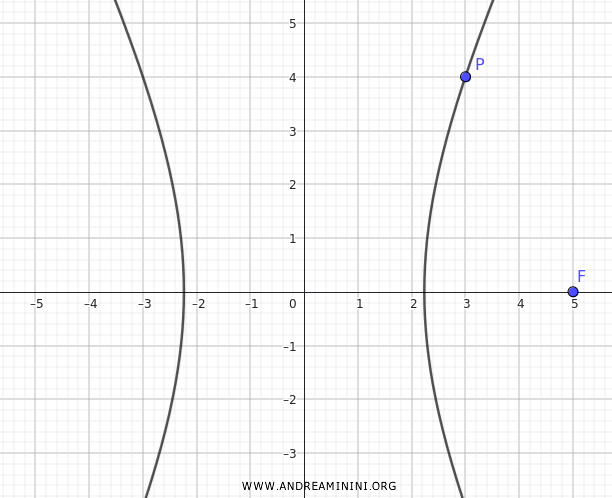
Method 2

Consider the same hyperbola centered at the origin that passes through the point \( P(3, 4) \) and has its focus at \( F(5, 0) \).

From the coordinates of the focus \( F(c,0) = (5,0) \), we know the distance from the focus to the center is \( c = 5 \).

Since the focus is on the x-axis, the standard equation of the hyperbola is:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

Next, determine the distance between the focus \( F \) and the point \( P \):

$$ \overline{PF} = \sqrt{(x_0 - c)^2 + (y_0 - 0)^2} $$

Where \( c = 5 \) and the coordinates of the point are \( x_0 = 3 \) and \( y_0 = 4 \):

$$ \overline{PF} = \sqrt{(3 - 5)^2 + 4^2} $$

$$ \overline{PF} = \sqrt{4 + 16} $$

$$ \overline{PF} = \sqrt{20} $$

$$ \overline{PF} = \sqrt{2^2 \cdot 5} $$

$$ \overline{PF} = 2 \sqrt{5} $$

If one focus is \( F(5, 0) \), the other focus will be \( F'(-5, 0) \).

Next, calculate the distance between the point \( P \) and the other focus \( F' \):

$$ PF' = \sqrt{(3 - (-5))^2 + (4 - 0)^2} $$

$$ PF' = \sqrt{8^2 + 4^2} $$

$$ PF' = \sqrt{64 + 16} $$

$$ PF' = \sqrt{80} $$

$$ PF' = \sqrt{2^4 \cdot 5} $$

$$ PF' = 2^2 \sqrt{5} $$

$$ PF' = 4 \sqrt{5} $$

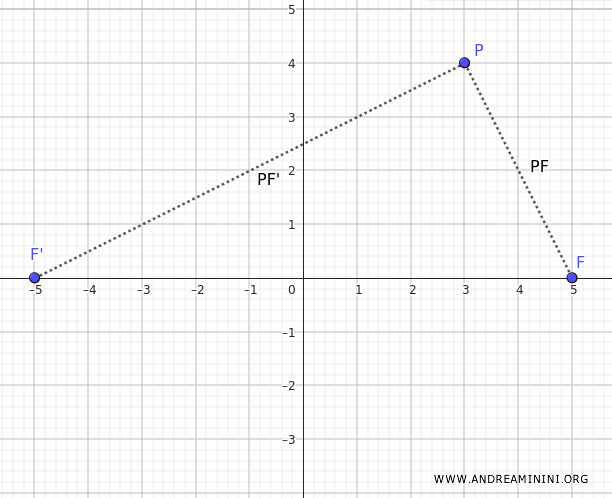
The hyperbola is the set of points such that the difference in distances from the two foci is constant and equal to \( 2a \), where \( 2a \) is the distance between the two vertices of the hyperbola. Thus:

$$ | PF - PF' | = 2a $$

Knowing that \( \overline{PF} = 2 \sqrt{5} \) and \( PF' = 4 \sqrt{5} \):

$$ | 2 \sqrt{5} - 4 \sqrt{5} | = 2a $$

$$ | -2 \sqrt{5} | = 2a $$

$$ 2 \sqrt{5} = 2a $$

$$ a = \sqrt{5} $$

Where \( a \) is the semi-distance between the vertices of the hyperbola.

In a hyperbola, the relationship between \( a \), \( b \) (semi-transverse axis), and \( c \) (focal distance) is given by:

$$ c^2 = a^2 + b^2 $$

Substitute \( c = 5 \) and \( a = \sqrt{5} \):

$$ 5^2 = (\sqrt{5})^2 + b^2 $$

$$ 25 = 5 + b^2 $$

$$ b^2 = 25 - 5 $$

$$ b^2 = 20 $$

$$ b = \sqrt{20} $$

Once we know \( a = \sqrt{5} \) and \( b = \sqrt{20} \), we substitute them into the standard equation of the hyperbola:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

$$ \frac{x^2}{(\sqrt{5})^2} - \frac{y^2}{(\sqrt{20})^2} = 1 $$

$$ \frac{x^2}{5} - \frac{y^2}{20} = 1 $$

This is the equation of the hyperbola that passes through the point \( (3, 4) \) and has one of its foci at \( (5, 0) \).