Finding the Equation of a Hyperbola Given a Point and Eccentricity

To determine the equation of a hyperbola centered at the origin, given the coordinates of a point $ P(x_0;y_0) $ and the eccentricity $ e $, follow these steps:

First, identify the transverse axis, which is the axis where the foci are located, using the additional information provided in the problem.

• If the transverse axis is the x-axis, the equation of the hyperbola is: $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ and the eccentricity is given by the formula $$ e = \frac{c}{a} $$
• If the transverse axis is the y-axis, the equation of the hyperbola is: $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$ and the eccentricity is given by the formula $$ e = \frac{c}{b} $$

Next, substitute the coordinates of the point $ P(x_0;y_0) $ into the hyperbola equation. Then, solve the resulting system of equations, which includes the eccentricity, to find the lengths of the transverse and conjugate axes.

An Example

Let’s consider a hyperbola centered at the origin that passes through the point $ P(-6; 2 \sqrt{15} )$ and has an eccentricity of $ e= \frac{\sqrt{7}}{2} $. In this case, the transverse axis, where the foci are located, is the y-axis.

Since the transverse axis is the y-axis, the equation of the hyperbola is:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$

The eccentricity is given by:

$$ e = \frac{c}{b} $$

We set up the following system of equations:

$$ \begin{cases} \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 \\ \\ e = \frac{c}{b} \end{cases} $$

Substituting the coordinates of the point $ P(-6; 2 \sqrt{15} )$ into the hyperbola equation gives:

$$ \begin{cases} \frac{(-6)^2}{a^2} - \frac{(2 \sqrt{15})^2}{b^2} = -1 \\ \\ e = \frac{c}{b} \end{cases} $$

This simplifies to:

$$ \begin{cases} \frac{36}{a^2} - \frac{60}{b^2} = -1 \\ \\ e = \frac{c}{b} \end{cases} $$

Now, substituting the given eccentricity $ e= \frac{\sqrt{7}}{2} $ into the system, we get:

$$ \begin{cases} \frac{36}{a^2} - \frac{60}{b^2} = -1 \\ \\ \frac{\sqrt{7}}{2} = \frac{c}{b} \end{cases} $$

Since for a hyperbola $ c^2 = a^2 + b^2 $, we can express $ c $ as $ \sqrt{a^2 + b^2} $:

$$ \begin{cases} \frac{36}{a^2} - \frac{60}{b^2} = -1 \\ \\ \frac{\sqrt{7}}{2} = \sqrt{ \frac{a^2 + b^2}{b^2} } \end{cases} $$

This further simplifies to:

$$ \begin{cases} \frac{36}{a^2} - \frac{60}{b^2} = -1 \\ \\ \frac{\sqrt{7}}{2} = \sqrt{ 1 + \frac{a^2}{b^2} } \end{cases} $$

Squaring both sides of the second equation yields:

$$ \begin{cases} \frac{36}{a^2} - \frac{60}{b^2} = -1 \\ \\ \frac{7}{4} = 1 + \frac{a^2}{b^2} \end{cases} $$

Solving for $ \frac{a^2}{b^2} $, we get:

$$ \begin{cases} \frac{36}{a^2} - \frac{60}{b^2} = -1 \\ \\ \frac{a^2}{b^2} = \frac{3}{4} \end{cases} $$

Substituting $ a^2 = \frac{3}{4} \cdot b^2 $ into the first equation gives:

$$ \begin{cases} \frac{36}{\frac{3}{4} \cdot b^2} - \frac{60}{b^2} = -1 \\ \\ a^2 = \frac{3}{4} \cdot b^2 \end{cases} $$

Rewriting the first equation:

$$ \begin{cases} \frac{144}{3b^2} - \frac{60}{b^2} = -1 \\ \\ a^2 = \frac{3}{4} \cdot b^2 \end{cases} $$

$$ \begin{cases} \frac{144 - 180}{3b^2} = -1 \\ \\ a^2 = \frac{3}{4} \cdot b^2 \end{cases} $$

$$ \begin{cases} \frac{-36}{3b^2} = -1 \\ \\ a^2 = \frac{3}{4} \cdot b^2 \end{cases} $$

$$ \begin{cases} \frac{-12}{b^2} = -1 \\ \\ a^2 = \frac{3}{4} \cdot b^2 \end{cases} $$

Solving for $ b^2 $, we find:

$$ \begin{cases} b^2 = 12 \\ \\ a^2 = \frac{3}{4} \cdot b^2 \end{cases} $$

Taking the square root:

$$ \begin{cases} b = \sqrt{12} \\ \\ a^2 = \frac{3}{4} \cdot b^2 \end{cases} $$

$$ \begin{cases} b = 2 \sqrt{3} \\ \\ a^2 = \frac{3}{4} \cdot b^2 \end{cases} $$

Now that we have the length of the transverse axis $ b = 2 \sqrt{3} $, substitute it back into the equation for $ a $:

$$ \begin{cases} b = 2 \sqrt{3} \\ \\ a^2 = \frac{3}{4} \cdot (2 \sqrt{3})^2 \end{cases} $$

$$ \begin{cases} b = 2 \sqrt{3} \\ \\ a^2 = \frac{3}{4} \cdot 12 \end{cases} $$

$$ \begin{cases} b = 2 \sqrt{3} \\ \\ a^2 = 9 \end{cases} $$

$$ \begin{cases} b = 2 \sqrt{3} \\ \\ a = 3 \end{cases} $$

Now that we know the lengths from the center to the vertices: $ b = 2 \sqrt{3} $ and $ a = 3 $, we can substitute these into the standard equation of the hyperbola:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$

$$ \frac{x^2}{9} - \frac{y^2}{12} = -1 $$

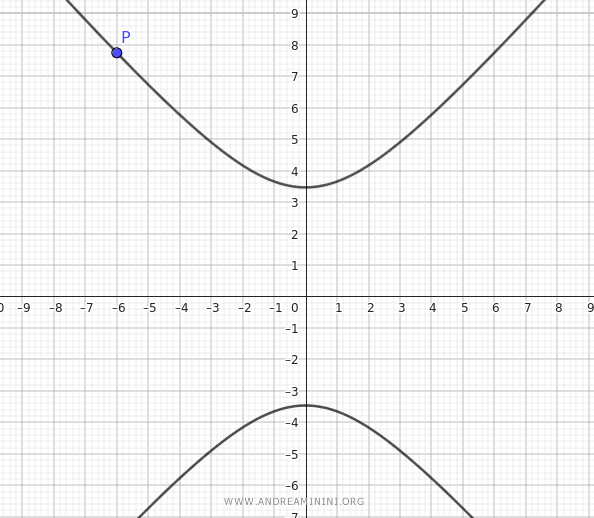
This is the equation of the hyperbola centered at the origin, passing through the point $ P(-6; 2 \sqrt{15} )$ with an eccentricity of $ e = \frac{\sqrt{7}}{2} $, where the transverse axis is the y-axis.

And that's it!