Ellipse
An ellipse is a plane figure defined as the set of points where the sum of the distances from two fixed points, F1 and F2, called foci, is constant and greater than the distance between the foci.
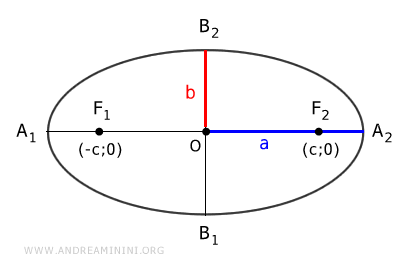
For an ellipse with foci F1 and F2, the sum of the distances PF1+PF2 is constant for any point P on the ellipse.
$$ \overline{PF_1} + \overline{PF_1} = 2a $$
For example, if we take any point P on the ellipse and add the distances from P to the foci F1 and F2, the result is always a constant value k=2a.
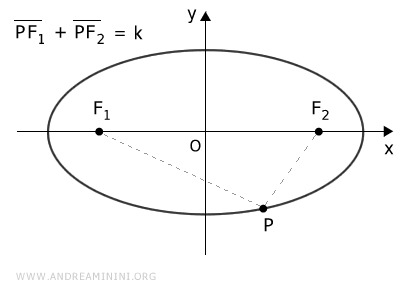
The focal distance $ \overline{F_1F_2} $ is the distance between the two foci and is always less than the sum of the distances PF1+PF2.
$$ \overline{PF_1} + \overline{PF_2} > \overline{F_1F_2} $$
Note. This is due to the triangle inequality theorem, which states that the sum of the lengths of any two sides of a triangle is greater than the length of the remaining side. Therefore, the side F1F2 is less than the sum of the other two sides PF1+PF2.
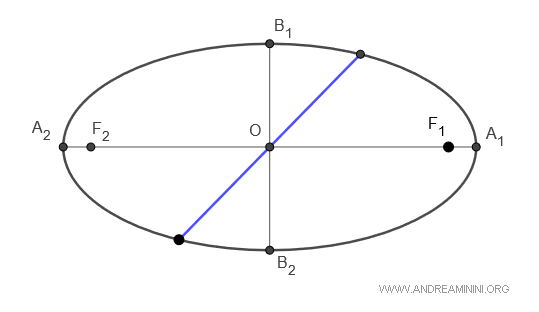
The axes of an ellipse are the two perpendicular lines A1A2 and B1B2 that pass through its center (O), called the major axis and minor axis, respectively.
- The major axis is the line passing through the foci and is the longest diameter.
- The minor axis is the line perpendicular to the major axis and is the shortest diameter.
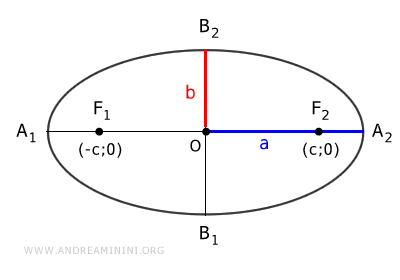
Thus, the focal distance is $ \overline{F_1F_2} = 2c $, the length of the major axis is $ \overline{A_1A_2} = 2a $ and the length of the minor axis is $ \overline{B_1B_2} = 2b $.
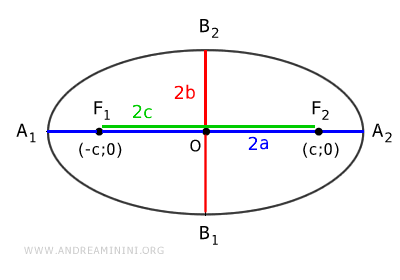
The midpoint of the major axis is called the center of the ellipse.
When the two axes are equal (a=b), the ellipse becomes a circle.
The points A1, A2, B1, and B2 are known as the vertices of the ellipse.
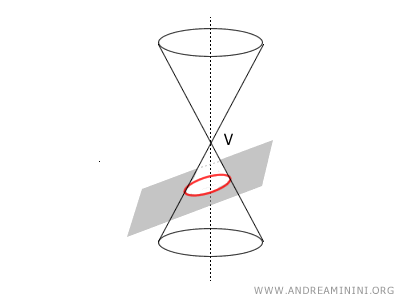
Geometrically, an ellipse is a conic section because it is formed by the intersection of a slanted plane with a cone, creating an angle between θ and π/2 with respect to the cone's axis.
Equation of an Ellipse
An ellipse has a standard formula, known as the canonical (or normal) equation of the ellipse, when centered at the origin of the Cartesian coordinate system:
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \]
Where "a" is half the length of the major axis and "b" is half the length of the minor axis, and x and y are the coordinates of any point P on the ellipse.
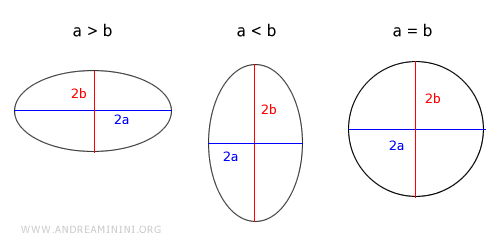
- If a > b, the ellipse is oriented along the x-axis
- If a < b, the ellipse is oriented along the y-axis
- If a = b, the ellipse is a circle
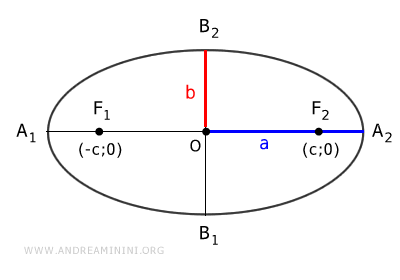
The formulas to find the coordinates of the foci of an ellipse depend on the relationship between the semi-axes "a" and "b".
- If a > b: $$ F_1 ( - \sqrt{ a^2 - b^2 } ;0 ) $$ $$ F_2 ( \sqrt{ a^2 - b^2 } ;0 ) $$
- If a < b: $$ F_1 (0; - \sqrt{ b^2 - a^2 } ) $$ $$ F_2 ( 0; \sqrt{ b^2 - a^2 } ) $$
Where "a" and "b" are the lengths of the semi-axes of the ellipse.
The vertices of the ellipse are found at the following coordinates (x;y):
$$ A_1 ( -a; 0) $$
$$ A_2 ( a; 0) $$
$$ B_1 ( 0; -b) $$
$$ B_2 ( 0; b) $$
These are the points where the ellipse intersects the Cartesian axes.
The more or less flattened shape of the ellipse is called eccentricity (e) and is determined by the following formula:
- If a > b the formula for eccentricity is $$ e = \frac{c}{a} $$
- If a < b the formula for eccentricity is $$ e = \frac{c}{b} $$
- If a = b either of the previous formulas can be used
Where "a" is the semi-major axis (half the length of the major axis 2a), "b" is the semi-minor axis (half the length of the minor axis 2b), and "c" is the focal distance (the distance from each focus to the center of the ellipse).
The distance "c" of each focus from the center of the ellipse is found using the Pythagorean theorem.
$$ c = \sqrt{a^2 -b^2} $$
In both cases, since c < a and c < b, we deduce that eccentricity is a parameter between 0 and 1.
$$ 0 \le e < 1 $$
The closer the eccentricity is to 1, the more elongated the ellipse is along the x-axis.
Conversely, the closer the eccentricity is to 0, the more the ellipse resembles a circle. With e=0, the ellipse becomes a circle.
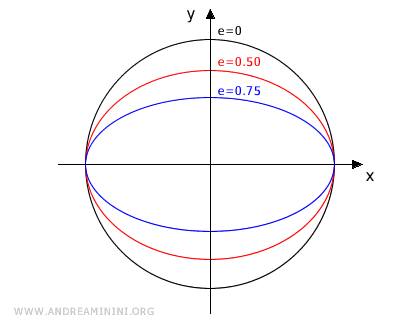
In other words, eccentricity can be seen as a measure of the "roundness" of the ellipse, ranging from 0 (a circle) to 1 (very elongated ellipses).
Note. Thus, a circle can be considered a special case of an ellipse where the two foci coincide with the center of the circle.
Every ellipse has two foci and two directrices, which are symmetric and perpendicular to the focal axis.
If the focal axis is the x-axis, the equations of the directrices are:
$$ x = \pm \frac{a^2}{c} $$
If the focal axis is the y-axis, the equations of the directrices are:
$$ y = \pm \frac{b^2}{c} $$
In general, as with any conic section, for any point $ P(x;y) $ on the ellipse, the ratio of the distance $ \overline{PF} $ from the point to a focus to the distance $ \overline{PH} $ from the point to a directrix is constant, and this constant is the eccentricity.
$$ e = \frac{ \overline{PF} }{ \overline{PH} } $$
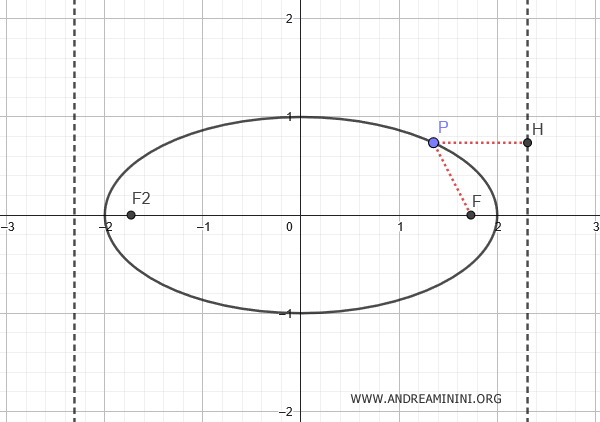
A Practical Example
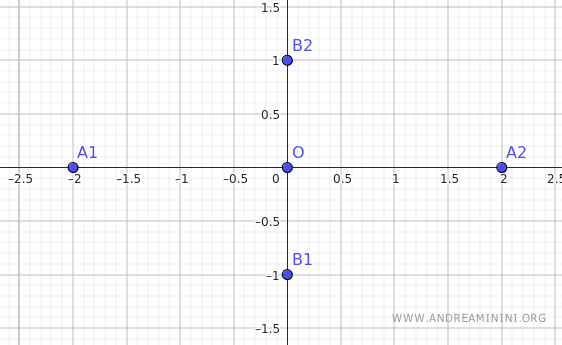
Let's construct an ellipse with horizontal and vertical semi-axes a=2 and b=1.
For simplicity, the center of the ellipse coincides with the origin of the Cartesian axes O(0;0).
Knowing that a=2 and b=1, the vertices of the ellipse are A1(-2;0), A2(2;0), B1(0;-1), B2(0;1).
To find the foci of the ellipse, we use the following formulas:
$$ \begin{cases} F_1 ( - \sqrt{ a^2 - b^2 } ;0 ) \\ \\ F_2 ( \sqrt{ a^2 - b^2 } ;0 ) \end{cases} $$
Substituting the values of the semi-axes a=2 and b=1 into both:
$$ \begin{cases} F_1 ( - \sqrt{ 2^2 - 1^2 } ;0 ) \\ \\ F_2 ( \sqrt{ 2^2 - 1^2 } ;0 ) \end{cases} $$
$$ \begin{cases} F_1 ( - \sqrt{ 4 - 1 } ;0 ) \\ \\ F_2 ( \sqrt{ 4 - 1 } ;0 ) \end{cases} $$
$$ \begin{cases} F_1 ( - \sqrt{ 3 } ;0 ) \\ \\ F_2 ( \sqrt{ 3 } ;0 ) \end{cases} $$
Therefore, the distance of the foci from the center of the ellipse is c=√3.
The two foci of the ellipse are located at the coordinates F1(-√3;0) and F2(√3;0).
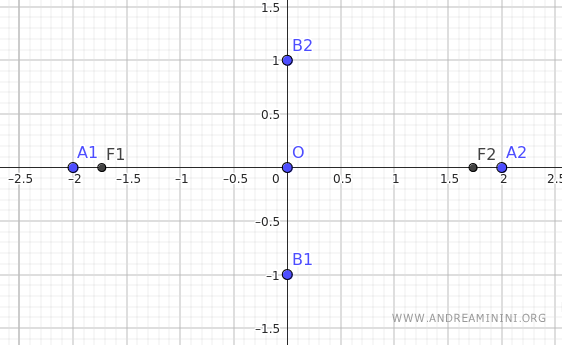
At this point, knowing the value of "c", we can calculate the eccentricity of the ellipse.
Since a > b, we use the following formula:
$$ e = \frac{c}{a} = \frac{ \sqrt{3} }{2} ≈ 0.86 $$
Finally, we use the canonical equation of the ellipse to find the various points on the ellipse.
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{2^2} + \frac{y^2}{1^2} = 1 $$
$$ \frac{x^2}{4} + y^2 = 1 $$
Solving for y:
$$ y^2 = 1-\frac{x^2}{4} $$
Then, we take the square root of both sides:
$$ \sqrt{y^2} = \sqrt{ 1-\frac{x^2}{4}} $$
$$ y = \pm \sqrt{ 1-\frac{x^2}{4}} $$
This form of the equation allows us to find the y-coordinate of any point given the x-coordinate in the range [-a,a], or [-2,2].
| x | y |
|---|---|
| -2 | 0 |
| -1 | ±0.86 |
| 0 | ±1 |
| 1 | ±0.86 |
| 2 | 0 |
These are the points we have just found.
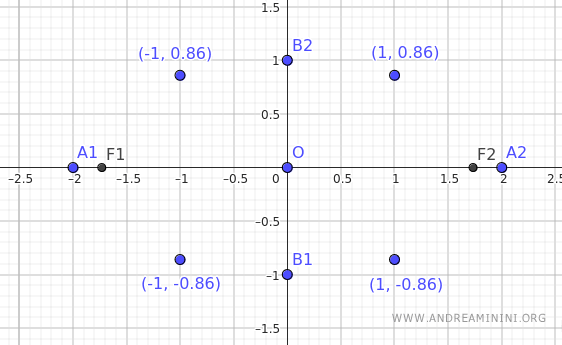
Even with these few points, we can start to imagine the shape of the ellipse.
By repeating the calculations, we can find more points on the ellipse to complete the drawing.
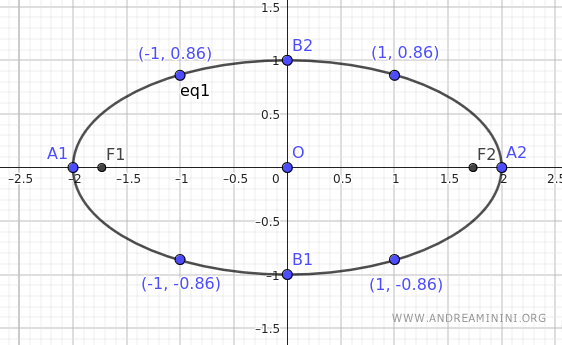
Note. In this example, I used Geogebra to construct the ellipse. It is a good method for learning the properties of the ellipse "hands-on" by experimenting with different values for the semi-axes.
Proof
The simplest ellipses have their center O at the origin of the Cartesian coordinate system and the foci on either the x-axis or the y-axis.
A] Ellipse with Foci on the x-axis
In this scenario, the foci are located on the x-axis, and the major axis is the horizontal axis, meaning a > b.
$$ a > b $$
Assume the foci are at coordinates F1(-c,0) and F2(c,0), equidistant from the ellipse's center.

The distance between the two foci is 2c.
$$ \overline{F_1F_2} = 2c $$
By definition, an ellipse is the set of points where the sum of the distances to the two foci is constant.
$$ \overline{PF_1} + \overline{PF_2} = k $$
What is the value of the constant k?
To find out, consider point A2 on the major axis x.
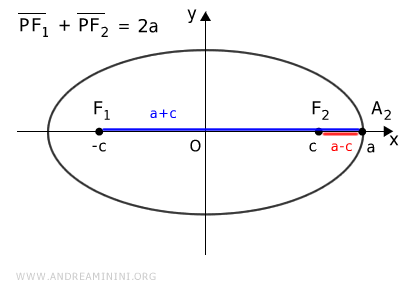
In this case, the distances from the foci are as follows.
$$ \overline{A_2F_1} = a+c $$
$$ \overline{A_2F_2} = a-c $$
Summing these distances, we get the value k=2a
$$ \overline{A_2F_1} + \overline{A_2F_2} = k $$
$$ (a+c) + (a-c) = k $$
$$ a+c + a-c = k $$
$$ 2a = k $$
Since k is constant for any point on the ellipse, we conclude that the sum of the distances PF1 + PF2 is always equal to 2a
$$ \overline{PF_1} + \overline{PF_2} = 2a $$
How do we find the coordinates of the foci?
To understand this, consider the vertex B2 on the minor axis y, knowing that k=2a.
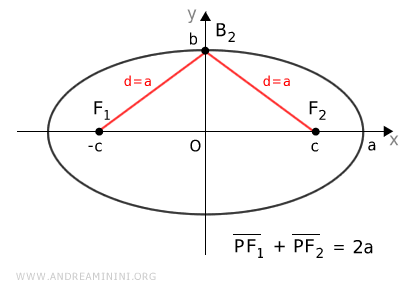
The sum of the distances from point B2 to the foci is equal to 2a.
$$ \overline{B_2F_1} + \overline{B_2F_2} = 2a $$
In this case, the distance to each focus is the same because point B2 lies on a symmetry axis of the ellipse.
$$ \overline{B_2F_1} = \overline{B_2F_2} = a $$
This means the distance (d=a) between a vertex on the y-axis and one of the foci is half the length of the major axis (2a).
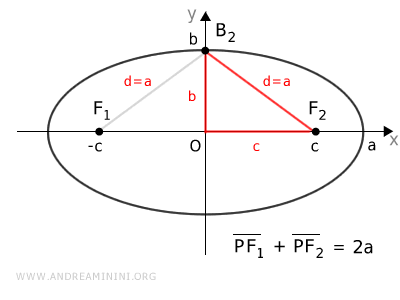
To calculate the value of c, apply the Pythagorean Theorem to the right triangle OB2F2, knowing that the hypotenuse is d=a and the legs are "a" and "c".
$$ a^2 = b^2 + c^2 $$
This allows us to derive the component "c"
$$ c^2 = a^2 - b^2 $$
$$ \sqrt{ c^2 } = \sqrt{ a^2 - b^2 } $$
$$ c = \sqrt{ a^2 - b^2 } $$
Therefore, the coordinates of the foci are
$$ F_1 ( - \sqrt{ a^2 - b^2 } ,0 ) $$
$$ F_2 ( \sqrt{ a^2 - b^2 } ,0 ) $$
How do we derive the equation of the ellipse?
Consider any point P(x,y) on the ellipse.
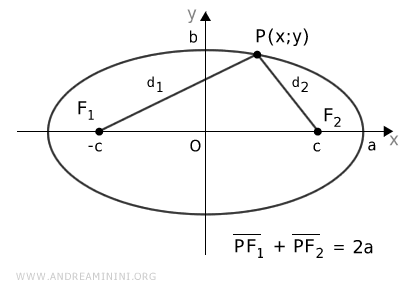
Using the Pythagorean theorem, we can calculate the distances from point P to the foci F1 and F2 of the ellipse.
$$ d_1 = \sqrt{(x+c)^2 + y^2} $$
$$ d_2 = \sqrt{(x-c)^2 + y^2} $$
Knowing that at any point P on the ellipse, the sum of the distances d1 + d2 is constant and equal to 2a:
$$ d_1 + d_2 = 2a $$
$$ \sqrt{(x+c)^2 + y^2} + \sqrt{(x-c)^2 + y^2} = 2a $$
If we manipulate the sum algebraically using the relation d1 + d2 = 2a and the Pythagorean theorem c2 = a2 - b2, after some simplifications and reworkings, we arrive at the canonical equation of the ellipse
Move one of the square roots to the right-hand side:
$$ \sqrt{(x+c)^2 + y^2} = 2a - \sqrt{(x-c)^2 + y^2} $$
Square both sides:
$$ ( \sqrt{(x+c)^2 + y^2} )^2 = ( 2a - \sqrt{(x-c)^2 + y^2} )^2 $$
$$ (x+c)^2 + y^2 = 4a^2 - 2 \cdot 2a \cdot \sqrt{(x-c)^2 + y^2} + ( \sqrt{(x-c)^2 + y^2} )^2 $$
$$ (x+c)^2 + y^2 = 4a^2 - 4a \cdot \sqrt{(x-c)^2 + y^2} + (x-c)^2 + y^2 $$
Expand the binomial squares:
$$ x^2 + 2xc + c^2 + y^2 = 4a^2 - 4a \cdot \sqrt{(x-c)^2 + y^2} + x^2 - 2xc + c^2 + y^2 $$
Then simplify:
$$ 2xc = 4a^2 - 4a \cdot \sqrt{(x-c)^2 + y^2} - 2xc $$
$$ 2xc + 2xc - 4a^2 = - 4a \cdot \sqrt{(x-c)^2 + y^2} $$
$$ 4xc - 4a^2 = - 4a \cdot \sqrt{(x-c)^2 + y^2} $$
Square both sides again to eliminate the square root:
$$ ( 4xc - 4a^2 )^2 = (- 4a \cdot \sqrt{(x-c)^2 + y^2} )^2 $$
$$ 16x^2c^2 + 16a^4 - 32a^2xc = 16 a^2 \cdot [ (x-c)^2 + y^2 ] $$
Divide both sides by 16:
$$ \frac{ 16x^2c^2 + 16a^4 - 32a^2xc}{16} = \frac{ 16 a^2 \cdot [ (x-c)^2 + y^2 ] } {16} $$
$$ x^2c^2 + a^4 - 2a^2xc = a^2 \cdot [ (x-c)^2 + y^2 ] $$
$$ \frac{ x^2c^2 + a^4 - 2a^2xc }{a^2} = (x-c)^2 + y^2 $$
$$ \frac{ x^2c^2}{a^2} + \frac{a^4}{a^2} - \frac{2a^2xc}{a^2} = (x-c)^2 + y^2 $$
$$ \frac{ x^2c^2}{a^2} + a^2 - 2xc = (x-c)^2 + y^2 $$
Expand the binomial square and simplify:
$$ \frac{ x^2c^2}{a^2} + a^2 - 2xc = x^2 + c^2 - 2xc + y^2 $$
$$ \frac{ x^2c^2}{a^2} + a^2 = x^2 + c^2 + y^2 $$
Move the known terms to the right side:
$$ \frac{ x^2c^2}{a^2} - x^2 - y^2 = c^2 - a^2 $$
$$ x^2 \cdot ( \frac{ c^2}{a^2} - 1) - y^2 = c^2 - a^2 $$
$$ x^2 \cdot ( \frac{ c^2 - a^2}{a^2}) - y^2 = c^2 - a^2 $$
Knowing that c2 = a2 - b2, replace c2 - a2 with -b2:
$$ x^2 \cdot \frac{ -b^2}{a^2} - y^2 = -b^2 $$
$$ - \frac{ x^2b^2}{a^2} - y^2 = -b^2 $$
Then multiply both sides by -1 to change the sign:
$$ [- \frac{ x^2b^2}{a^2} - y^2 ] \cdot (-1) = -b^2 \cdot (-1) $$
$$ \frac{ x^2b^2}{a^2} + y^2 = b^2 $$
Finally, divide both sides by b2:
$$ \frac{1}{b^2} \cdot [ \frac{ x^2b^2}{a^2} + y^2 ] = \frac{1}{b^2} \cdot b^2 $$
$$ \frac{ x^2b^2}{a^2b^2} + \frac{y^2}{b^2} = 1 $$
The final result is the canonical equation of the ellipse.
$$ \frac{ x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
Where x and y are the coordinates of any point P on the ellipse, while a and b are the lengths of the ellipse's semi-axes.
Alternate Proof Development. Once reaching the equation
$$ 4xc - 4a^2 = - 4a \cdot \sqrt{(x-c)^2 + y^2} $$
Divide both sides by four:
$$ xc - a^2 = - a \cdot \sqrt{(x-c)^2 + y^2} $$
Multiply both sides by -1:
$$ a^2 - xc = a \cdot \sqrt{(x-c)^2 + y^2} $$
Square both sides of the equation:
$$ (a^2 - xc)^2 = (a \cdot \sqrt{(x-c)^2 + y^2})^2 $$
$$ (a^2 - xc)^2 = a^2 \cdot [(x-c)^2 + y^2] $$
$$ a^4 - 2a^2xc + x^2c^2 = a^2 \cdot (x^2 - 2xc + c^2 + y^2) $$
$$ \require{cancel} a^4 - \cancel{2a^2xc} + x^2c^2 = a^2x^2 - \cancel{2a^2xc} + a^2c^2 + a^2y^2 $$
$$ a^4 - a^2c^2 = a^2x^2 - x^2c^2 + a^2y^2 $$
$$ a^2 (a^2 - c^2) = x^2 (a^2 - c^2) + a^2y^2 $$
Knowing that $ a^2 - c^2 = b^2 $$$ a^2 (b^2) = x^2 (b^2) + a^2y^2 $$
$$ a^2b^2 = b^2x^2 + a^2y^2 $$
Divide both sides by $ a^2b^2 $
$$ \frac{ a^2b^2 }{a^2b^2} = \frac{ b^2x^2 + a^2y^2 }{a^2b^2} $$
$$ 1 = \frac{ b^2x^2 }{a^2b^2} + \frac{ a^2y^2 }{a^2b^2} $$
$$ 1 = \frac{ x^2 }{a^2} + \frac{ y^2 }{b^2} $$
This is the canonical (or standard) equation of the ellipse that I aimed to prove:
$$ \frac{ x^2 }{a^2} + \frac{ y^2 }{b^2} = 1 $$
B] Ellipse with Foci on the y-axis
In this scenario, the foci are located on the y-axis, and the vertical axis of the ellipse is longer than the horizontal axis. Therefore, the starting hypothesis is:
$$ b > a $$
The two foci are at coordinates F1(0,-c) and F2(0,c), equidistant from the ellipse's center.
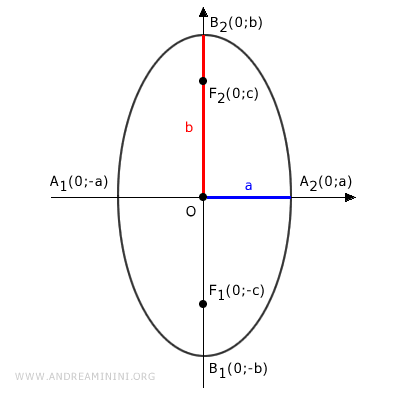
The length of the major axis is 2b.
Therefore, the sum of the distances from any point P must be equal to 2b.
$$ \overline{PF_1} + \overline{PF_2} =2b $$
The proof that the sum is equal to 2b is similar to the previous case.
If we consider point B2, the distances to the two foci are as follows:
$$ \overline{B_2F_1} = b+c $$
$$ \overline{B_2F_2} = b-c $$
Summing these distances, we get the value k=2b
$$ \overline{B_2F_1} + \overline{B_2F_2} = k $$
$$ ( b+c) + (b-c) = k $$
$$ b+c + b-c = k $$
$$ 2b = k $$
Knowing that in an ellipse the sum of the distances from the foci is always constant, we deduce that the sum is 2b at every point on the ellipse.
Since b > a, in this case, the foci of the ellipse are on the y-axis:
$$ F_1 (0; - \sqrt{ b^2 - a^2 } ) $$ $$ F_2 ( 0; \sqrt{ b^2 - a^2 } ) $$
The canonical equation to describe the ellipse remains the same:
$$ \frac{ x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
The same properties and considerations made in the previous proof apply here.
History of the Ellipse
The ellipse was first studied by Greek mathematicians.
In the 4th century BC, Menaechmus, a student of Eudoxus and contemporary of Plato, is known for discovering conic sections, including the ellipse. He obtained the ellipse by intersecting a cone with a plane inclined not parallel to the base.

The most significant contribution to the theory of conics was made in the 3rd century BC by Apollonius, who wrote an eight-book work called "Conics." Apollonius systematized and expanded existing knowledge on conics, introducing the terms ellipse, parabola, and hyperbola. He was also the first to derive all conics from a single cone. Previously, different cones were used to obtain the various conics.
During the Middle Ages, the mathematical knowledge of the ancient Greeks was preserved and developed by Arab scholars. The ellipse continued to be studied, and Greek works were translated into Arabic and later into Latin.
In the 17th century, the ellipse became fundamental in describing planetary orbits. Kepler discovered that the orbits of planets around the Sun were not circular but elliptical.
With the development of analytic geometry, René Descartes introduced the concept of Cartesian coordinates, allowing the algebraic representation of curves. The standard equation of the ellipse, \( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \), derives from this approach.
Subsequently, the ellipse found applications in numerous fields of science and engineering. For example, elliptical mirrors and the study of elliptical trajectories of objects moving under the influence of central forces.
Symmetry of the Ellipse
The ellipse has the geometric property of being symmetrical with respect to its two main axes (major axis and minor axis).
The symmetry of the ellipse implies that for every point on the ellipse, there is another point located symmetrically with respect to the major and minor axes.
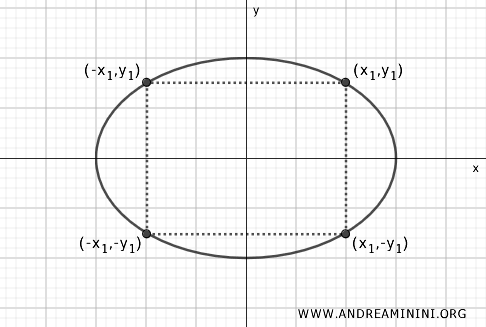
Note. This property arises from the fact that the variables x and y are squared. The square of a number is always equal to the square of its opposite. Therefore $ x^2 = (-x^2) $ and $ y^2 = (-y)^2 $. This means that the ellipse has as its symmetry axes both the x-axis $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \Leftrightarrow \frac{(-x)^2}{a^2} + \frac{y^2}{b^2} = 1 $$ and the y-axis $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \Leftrightarrow \frac{x^2}{a^2} + \frac{(-y)^2}{b^2} = 1 $$
There are three types of symmetries in the ellipse:
- Symmetry with respect to the y-axis
Consider a point \( P(x, y) \) on the ellipse. The point symmetrical with respect to the y-axis is \( P'(-x, y) \). This property means that the ellipse is identical if reflected along the y-axis.
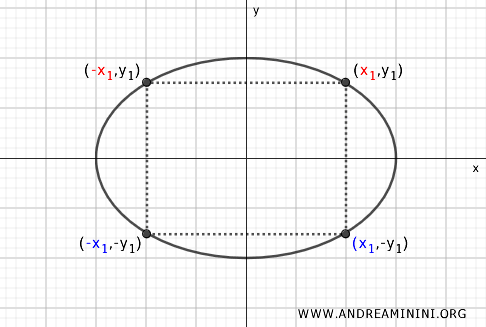
- Symmetry with respect to the x-axis
Similarly, for a point \( P(x, y) \), the point symmetrical with respect to the x-axis is \( P'(x, -y) \). Here too, the ellipse maintains its shape if reflected along the x-axis.
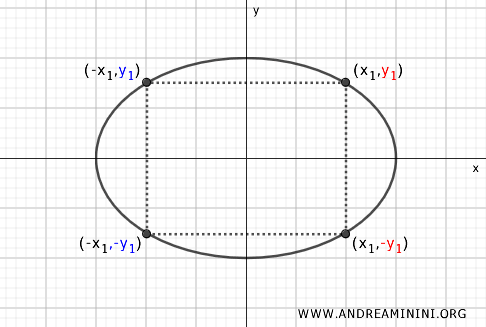
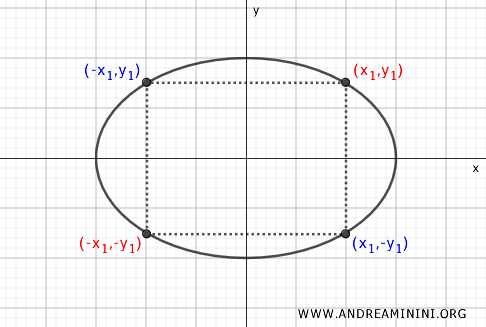
- Symmetry with respect to the origin
Another aspect of the ellipse's symmetry is that for a point \( P(x, y) \), there is a point symmetrical with respect to the center, given by \( P'(-x, -y) \). This means that the ellipse can be reflected with respect to the origin and will appear identical.
Notes
Some notes and observations on ellipses:
- The ellipse is inscribed in a rectangle
Every ellipse is inscribed in a rectangle that passes through the vertices and has sides of length 2a and 2b.
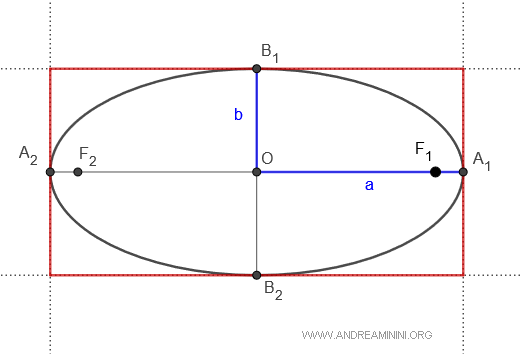
- The ellipse is a conic
The ellipse belongs to the family of conics, like hyperbolas, circles, and parabolas, because it can be obtained as a section by intersecting an inclined plane with a circular cone. - If the eccentricity is zero, the ellipse becomes a circle
If the ellipse has an eccentricity of zero (e=0), it coincides with a circle, and the two foci are both at the center of the circle. - The diameter of the ellipse
Any chord passing through the center of the ellipse is called a "diameter".
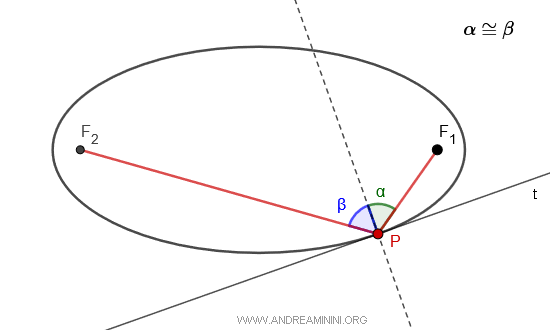
- The Focal Property of an Ellipse
At any point P on an ellipse, the angle bisector of the lines joining P with the foci F1 and F2 stands perpendicular to the tangent at point P on the curve. This means the focal radii $ \overline{PF_1} $ and $ \overline{PF_2} $ connecting the foci to point P on the ellipse form two congruent angles $ \alpha \cong \beta $ with the perpendicular to the tangent line (t) at P.
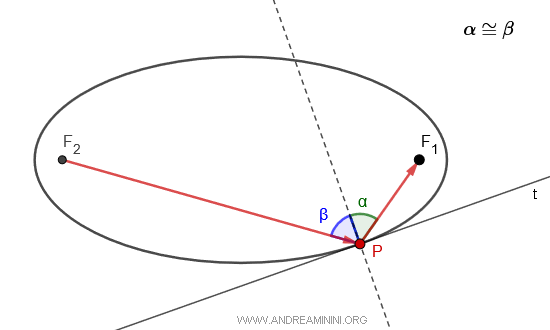
Therefore, any light source emanating from one focus toward point P will be reflected towards the other focus.
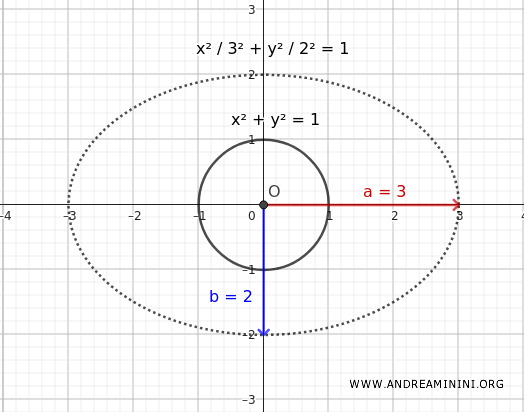
- An ellipse is a stretched circle
The equation of a circle centered at the origin is $$ x^2 + y^2 = 1 $$. By applying a dilation of $ ax $ and $ by $ to the variables, we get $$ \begin{cases} x' = ax \\ \\ y' = by \end{cases} $$. Solving for $ x $ and $ y $, we have $$ \begin{cases} x = \frac{x'}{a} \\ \\ y = \frac{y'}{b} \end{cases} $$. Substituting $ x $ and $ y $ back into the circle's equation $$ x^2 + y^2 = 1 $$ results in $$ \left(\frac{x'}{a}\right)^2 + \left(\frac{y'}{b}\right)^2 = 1 $$ $$ \frac{x'^2}{a^2} + \frac{y'^2}{b^2} = 1 $$. This is the standard equation of an ellipse centered at the origin.
The ratio of the areas is proportional. The area $ s $ of the circle centered at the origin and the area $ s' $ of the ellipse obtained by a dilation of $ a $ and $ b $ are proportional: $$ s' = s \cdot ab $$ where $ s = \pi \cdot 1^2 = \pi $ if the circle has a unit radius. Consequently, the area of the ellipse is: $$ s' = \pi \cdot ab $$
And so on.
