How to Find the Equation of an Ellipse Given the Semi-Axes

When you know the lengths of an ellipse's semi-axes, you can easily determine its equation. There are two main scenarios to consider:

• Ellipse Centered at the Origin (0, 0)
  If the ellipse is centered at the origin of the Cartesian coordinate system, its equation is simply given by the lengths \(a\) of the horizontal semi-axis and \(b\) of the vertical semi-axis: $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
• Ellipse Centered at a Point \((h, k)\)
  If the ellipse is centered at a point \( P(h,k) \), the equation is: $$ \frac{(x - h)^2}{a^2} + \frac{(y - k)^2}{b^2} = 1 $$ where \(a\) is the length of the horizontal semi-axis and \(b\) is the length of the vertical semi-axis.

Example

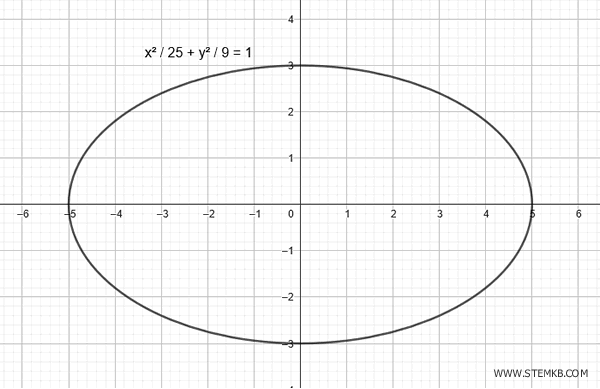
Let's consider an ellipse centered at the origin with a horizontal semi-axis \(a = 5\) and a vertical semi-axis \(b = 3\).

The equation of the ellipse is:

$$ \frac{x^2}{5^2} + \frac{y^2}{3^2} = 1 $$

$$ \frac{x^2}{25} + \frac{y^2}{9} = 1 $$

Here is the graph of the ellipse:

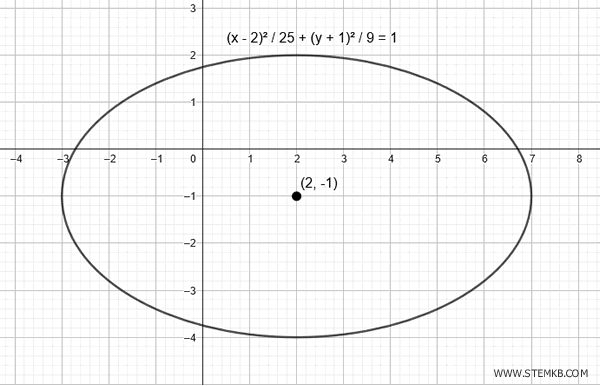
If the ellipse is centered at the point \((2, -1)\) with the same semi-axes, the equation is:

$$ \frac{(x - 2)^2}{25} + \frac{(y + 1)^2}{9} = 1 $$

Here is the graph of the translated ellipse:

These general formulas apply to any ellipse, as long as you know the lengths of the semi-axes and the position of the center.

And so on.