Equation of an Ellipse Not Centered at the Origin of the Cartesian Axes
The equation of an ellipse with its center at (x0, y0), away from the origin of the Cartesian axes, is given by $$ \frac{(x-x_0)^2}{a^2} + \frac{(y-y_0)^2}{b^2} = 1 $$. This is known as the translated standard form.
Alternatively, the equation of an ellipse not centered at the origin can also be written in this general form:
$$ Ax^2 + By^2 + Cx + Dy + E = 0 $$
Where:
$$ A = b^2 $$
$$ B = a^2 $$
$$ C = -2b^2x_0 $$
$$ D = -2a^2y_0 $$
$$ E = b^2x_0^2 + a^2y_0^2 - a^2b^2 $$
The coordinates of the center of the translated ellipse are:
$$ O \left( - \frac{C}{2A} ; - \frac{D}{2B} \right) $$
Thus, the axes of symmetry of the ellipse are:
$$ x = - \frac{C}{2A} $$
$$ y = - \frac{D}{2B} $$
In other words, an ellipse with a center not at the origin is simply a translated version of an ellipse centered at the origin.
A Practical Example
Consider an ellipse with semi-axes \(a = 3\) and \(b = 2\), and the center at \((x_0, y_0) = (1, -2)\).
The equation of the ellipse in the translated standard form with \( x_0 = 1 \) and \( y_0 = -2 \) is:
$$ \frac{(x - x_0)^2}{a^2} + \frac{(y - y_0)^2}{b^2} = 1 $$
$$ \frac{(x - 1)^2}{3^2} + \frac{(y + 2)^2}{2^2} = 1 $$
$$ \frac{(x - 1)^2}{9} + \frac{(y + 2)^2}{4} = 1 $$
Here is the graphical representation:
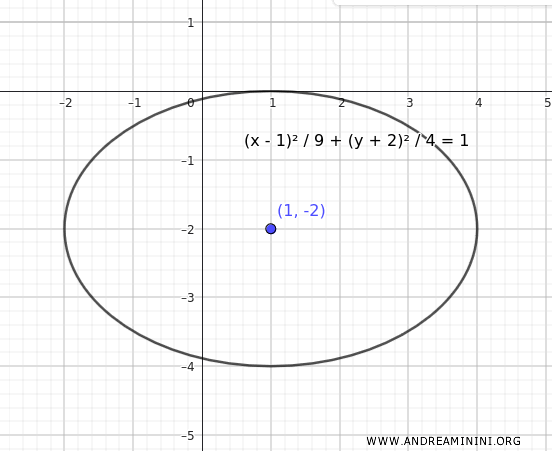
Note that this ellipse is simply a translation of an ellipse centered at the origin.

Next, let's convert this equation to the general form:
$$ Ax^2 + By^2 + Cx + Dy + E = 0 $$
Where:
$$ A = b^2 = 2^2 = 4 $$
$$ B = a^2 = 3^2 = 9 $$
$$ C = -2b^2x_0 = -2 \cdot 4 \cdot 1 = -8 $$
$$ D = -2a^2y_0 = -2 \cdot 9 \cdot (-2) = 36 $$
$$ E = b^2x_0^2 + a^2y_0^2 - a^2b^2 = 4 \cdot 1^2 + 9 \cdot (-2)^2 - 9 \cdot 4 $$
$$ E = 4 \cdot 1 + 36 - 36 $$
$$ E = 4 $$
Therefore, the general form of the ellipse's equation is:
$$ 4x^2 + 9y^2 - 8x + 36y + 4 = 0 $$
Graphically, the representation remains the same.
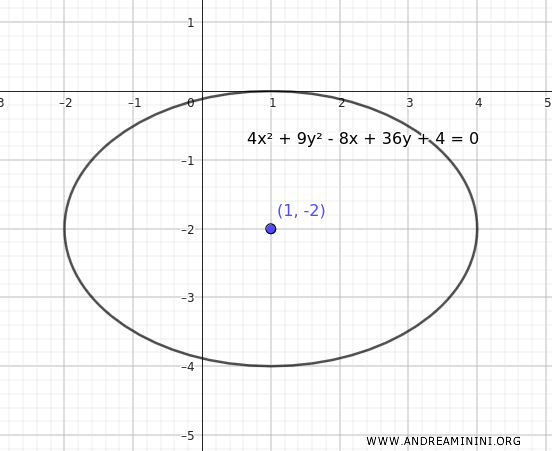
To verify that the center of the ellipse is indeed \((1, -2)\), we use the formulas for the center \((h, k)\):
$$ h = -\frac{C}{2A} = -\frac{-8}{2 \cdot 4} = \frac{8}{8} = 1 $$
$$ k = -\frac{D}{2B} = -\frac{36}{2 \cdot 9} = -\frac{36}{18} = -2 $$
The coordinates of the center are confirmed: \((1, -2)\).
Thus, we have verified that both forms of the equation describe the same ellipse with center \((1, -2)\), semi-axes \(a = 3\) and \(b = 2\).
The Proof
To prove the standard and general equations of an ellipse not centered at the origin, we start from the equation of an ellipse centered at the origin:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
Next, we apply a geometric transformation to shift all points of the ellipse, ensuring that the points maintain the same distances between each other (isometry).
In this case, we use a translation:
$$ \begin{cases} x' = x + x_0 \\ y' = y + y_0 \end{cases} $$
Where x' and y' are the new coordinates of each point (x, y), and x0 and y0 measure the horizontal and vertical shifts.
We derive the values of x' and y':
$$ \begin{cases} x = x' - x_0 \\ y = y' - y_0 \end{cases} $$
Substitute \( x = x' - x_0 \) and \( y = y' - y_0 \) into the standard equation of the ellipse:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{(x' - x_0)^2}{a^2} + \frac{(y' - y_0)^2}{b^2} = 1 $$
This yields the standard equation of the ellipse centered at \((x_0, y_0)\).
Next, we perform the algebraic calculations:
$$ \frac{x'^2 - 2x'x_0 + x_0^2}{a^2} + \frac{y'^2 - 2y'y_0 + y_0^2}{b^2} = 1 $$
$$ \frac{b^2 (x'^2 - 2x'x_0 + x_0^2) + a^2 (y'^2 - 2y'y_0 + y_0^2) }{a^2b^2} = 1 $$
$$ b^2 (x'^2 - 2x'x_0 + x_0^2) + a^2 (y'^2 - 2y'y_0 + y_0^2) = a^2b^2 $$
$$ b^2 (x'^2 - 2x'x_0 + x_0^2) + a^2 (y'^2 - 2y'y_0 + y_0^2) - a^2b^2 = 0 $$
$$ x'^2b^2 - 2x'x_0b^2 + x_0^2b^2 + y'^2a^2 - 2y'y_0a^2 + y_0^2a^2 - a^2b^2 = 0 $$
$$ x'^2 \cdot (b^2) + y'^2 \cdot (a^2) + x' \cdot ( - 2x_0b^2 ) + y' \cdot ( - 2y_0a^2 ) + x_0^2b^2 + y_0^2a^2 - a^2b^2 = 0 $$
Now, we substitute \( A = b^2 \), \( B = a^2 \), \( C = -2b^2x_0 \), \( D = -2a^2y_0 \), \( E = b^2x_0^2 + a^2y_0^2 - a^2b^2 \)
$$ x'^2 \cdot A + y'^2 \cdot B + x' \cdot C + y' \cdot D + E = 0 $$
$$ Ax'^2 + By'^2 + Cx' + Dy' + E = 0 $$
Thus, we have derived the general form of the equation for an ellipse centered at \((x_0, y_0)\).
And so on.
