How to Determine the Equation of an Ellipse Given a Point and Eccentricity

To determine the equation of an ellipse centered at the origin, given a point's coordinates and the ellipse's eccentricity, substitute the point's coordinates into the general equation of the ellipse:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

Depending on whether the major axis is horizontal or vertical, use the corresponding formula for eccentricity:

• If the major axis is horizontal (a > b): $$ e = \sqrt{1 - \frac{b^2}{a^2} } $$
• If the major axis is vertical (b > a): $$ e = \sqrt{1 - \frac{a^2}{b^2} } $$

Set up a system of equations and solve for the unknown values.

Note: If the major axis is unknown, both scenarios must be considered.

A Practical Example

Consider an ellipse passing through the point \((1, -\sqrt{3})\) with an eccentricity \( e = \frac{\sqrt{3}}{3} \).

Since the major axis is unknown, we need to analyze both scenarios.

1] First Case: \(a\) is the Major Axis (a > b)

For a horizontal major axis (a > b), the eccentricity formula is:

$$ e = \sqrt{1 - \frac{b^2}{a^2}} = \frac{\sqrt{3}}{3} $$

Square both sides of the equation:

$$ \left( \sqrt{1 - \frac{b^2}{a^2}} \right)^2 = \left( \frac{\sqrt{3}}{3} \right)^2 $$

$$ 1 - \frac{b^2}{a^2} = \frac{3}{9} $$

$$ 1 - \frac{b^2}{a^2} = \frac{1}{3} $$

$$ - \frac{b^2}{a^2} = \frac{1}{3} - 1 $$

$$ - \frac{b^2}{a^2} = \frac{1-3}{3} $$

$$ - \frac{b^2}{a^2} = - \frac{2}{3} $$

Multiply both sides by -1:

$$ \frac{b^2}{a^2} = \frac{2}{3} $$

$$ b^2 = \frac{2}{3} a^2 $$

Take the square root of both sides:

$$ \sqrt{ b^2 } = \sqrt{ \frac{2}{3} a^2 } $$

$$ b = a \sqrt{\frac{2}{3}} $$

Now substitute the known point \((1, -\sqrt{3})\) into the general equation of the ellipse:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

$$ \frac{1^2}{a^2} + \frac{(-\sqrt{3})^2}{b^2} = 1 $$

Knowing \( b = a \sqrt{\frac{2}{3}} \), substitute \( b \):

$$ \frac{1}{a^2} + \frac{3}{(a \cdot \sqrt{ \frac{2}{3} })^2} = 1 $$

$$ \frac{1}{a^2} + \frac{3}{a^2 \cdot \frac{2}{3}} = 1 $$

$$ \frac{1}{a^2} + \frac{3}{\frac{2}{3} a^2} = 1 $$

$$ \frac{1}{a^2} + 3 \cdot \frac{3}{2a^2} = 1 $$

$$ \frac{1}{a^2} + \frac{9}{2 a^2} = 1 $$

$$ \frac{2+9}{2 a^2} = 1 $$

$$ \frac{11}{2 a^2} = 1 $$

$$ 2 a^2 = 11 $$

$$ a^2 = \frac{11}{2} $$

$$ a = \sqrt{\frac{11}{2}} $$

Once we have \( a = \sqrt{\frac{11}{2}} \), we can calculate \( b \):

$$ b = a \sqrt{\frac{2}{3}} $$

$$ b = \sqrt{\frac{11}{2}} \sqrt{\frac{2}{3}} $$

$$ b = \sqrt{ \frac{11}{2} \cdot \frac{2}{3} } $$

$$ b = \sqrt{ \frac{11}{3} } $$

So, the equation of the ellipse with \( a = \sqrt{\frac{11}{2}} \) and \( b = \sqrt{ \frac{11}{3} } \) is:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

$$ \frac{x^2}{( \sqrt{\frac{11}{2}} )^2} + \frac{y^2}{( \sqrt{ \frac{11}{3} } )^2} = 1 $$

$$ \frac{x^2}{ \frac{11}{2} } + \frac{y^2}{ \frac{11}{3} } = 1 $$

$$ \frac{2x^2}{ 11 } + \frac{3y^2}{ 11 } = 1 $$

Here is the graphical representation:

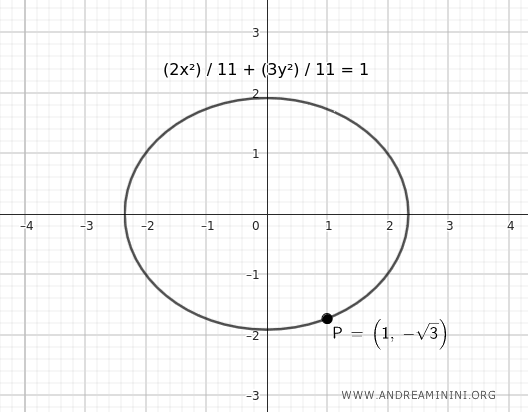
The ellipse passes through the given point.

2] Second Case: \(a\) is the Minor Axis (a < b)

When \( b \) is the major axis, the eccentricity formula is:

$$ e = \sqrt{1 - \frac{a^2}{b^2}} = \frac{\sqrt{3}}{3} $$

Square both sides of the equation:

$$ \left( \sqrt{1 - \frac{a^2}{b^2}} \right)^2 = \left( \frac{\sqrt{3}}{3} \right)^2 $$

$$ 1 - \frac{a^2}{b^2} = \frac{3}{9} $$

$$ 1 - \frac{a^2}{b^2} = \frac{1}{3} $$

$$ - \frac{a^2}{b^2} = \frac{1}{3} - 1 $$

$$ - \frac{a^2}{b^2} = \frac{1-3}{3} $$

$$ - \frac{a^2}{b^2} = - \frac{2}{3} $$

Multiply both sides by -1:

$$ \frac{a^2}{b^2} = \frac{2}{3} $$

$$ a = b \sqrt{\frac{2}{3}} $$

Now substitute the known point \((1, -\sqrt{3})\) into the general equation of the ellipse:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

$$ \frac{1^2}{a^2} + \frac{(-\sqrt{3})^2}{b^2} = 1 $$

Knowing \( a = b \sqrt{\frac{2}{3}} \):

$$ \frac{1}{( b \sqrt{\frac{2}{3}} )^2} + \frac{3}{b^2} = 1 $$

$$ \frac{1}{b^2 \cdot \frac{2 }{3}} + \frac{3}{b^2} = 1 $$

$$ \frac{3}{2 b^2} + \frac{3}{b^2} = 1 $$

$$ \frac{3+6}{2 b^2} = 1 $$

$$ \frac{9}{2 b^2} = 1 $$

$$ 2 b^2 = 9 $$

$$ b^2 = \frac{9}{2} $$

$$ b = \sqrt{\frac{9}{2}} $$

$$ b = \frac{3}{\sqrt{2}} $$

Multiply and divide by the square root of 2:

$$ b = \frac{3}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} $$

$$ b = \frac{3 \sqrt{2}}{2} $$

Once we have \( b = \frac{3 \sqrt{2}}{2} \), we can calculate \( a \):

$$ a = b \sqrt{\frac{2}{3}} $$

$$ a = \frac{3 \sqrt{2}}{2} \cdot \sqrt{\frac{2}{3}} $$

$$ a = \frac{3 \sqrt{2}}{2} \cdot \sqrt{\frac{2}{3}} $$

$$ a = \frac{3 \sqrt{2}}{2} \cdot \frac{\sqrt{2}}{\sqrt{3}} $$

$$ a = \frac{3 \cdot 2}{2 \sqrt{3}} $$

$$ a = \frac{3}{\sqrt{3}} $$

$$ a = \frac{3}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} $$

$$ a = \frac{3 \sqrt{3}}{\sqrt{3} \sqrt{3}} $$

$$ a = \frac{3 \sqrt{3}}{3} $$

$$ a = \sqrt{3} $$

Now we can substitute \( a = \sqrt{3} \) and \( b = \frac{3 \sqrt{2}}{2} \) into the general equation of the ellipse:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

$$ \frac{x^2}{( \sqrt{3} )^2} + \frac{y^2}{( \frac{3 \sqrt{2}}{2} )^2} = 1 $$

$$ \frac{x^2}{3} + \frac{y^2}{ \frac{9 \cdot 2}{4} } = 1 $$

$$ \frac{x^2}{3} + \frac{y^2}{ \frac{9}{2} } = 1 $$

$$ \frac{x^2}{3} + \frac{2y^2}{ 9 } = 1 $$

This is the equation of the ellipse if \(b\) is the major axis.

Here is the graphical representation:

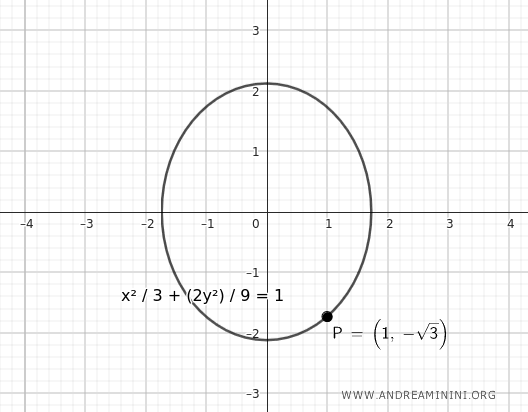
Thus, the ellipse passing through the point \((1, -\sqrt{3})\) with an eccentricity of \(\frac{\sqrt{3}}{3}\) can be described by either of the above equations, depending on which assumption (major or minor axis) is correct.

And so on.