Tangent Lines to an Ellipse Passing Through a Point P

Given an ellipse and any point P in the plane, there can be two, one, or no tangent lines to the ellipse passing through point P.

• If point P is outside the ellipse, there are two tangent lines to the ellipse passing through P.
  
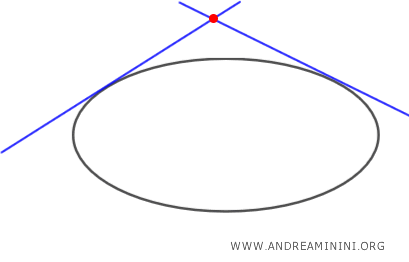
• If point P is on the ellipse, there is exactly one tangent line to the ellipse passing through P.
  
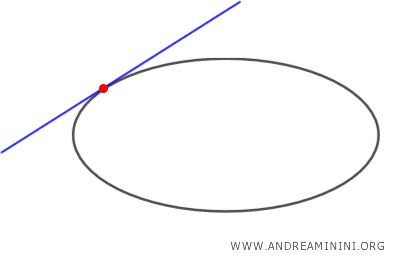
• If point P is inside the ellipse, there are no tangent lines to the ellipse passing through P.
  

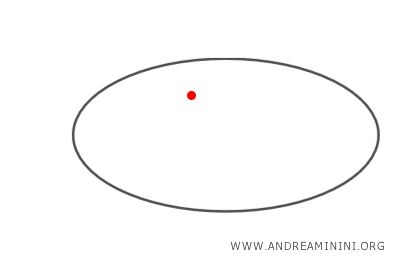
How to Find Tangent Lines to the Ellipse

To find the equation of the tangent lines to the ellipse passing through P, start by writing the equation of the family of lines passing through the point P(x₀, y₀).

$$ y - y_0 = m(x - x_0) $$

Next, write the equation of the ellipse:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

Now, determine which lines from this family intersect the ellipse.

Create a system of equations with these two equations:

$$ \begin{cases} y - y_0 = m(x - x_0) \\ \\ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \end{cases} $$

The solutions to this system represent all points of intersection (both tangent and secant) between the line and the ellipse.

Knowing that tangent lines have a zero discriminant (a unique solution), add the condition $ \Delta = 0 $ to identify only the tangent lines.

$$ \Delta = b^2 - 4ac = 0 $$

This condition allows us to find the slope \( m \) of the tangent lines to the ellipse, if they exist.

Once the slope \( m \) is found, substitute it back into the equation of the family of lines to find the equation of the tangent line.

A Practical Example

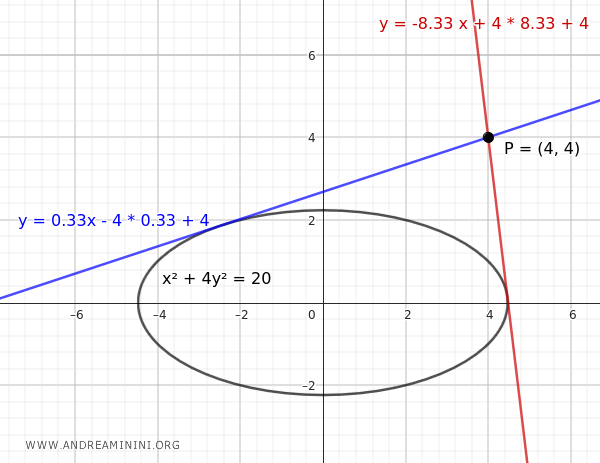
Consider a point P(4, 4) and the ellipse:

$$ x^2 + 4y^2 = 20 $$

We need to determine if there are tangent lines to the ellipse passing through point P(4, 4) and, if so, find their equations.

Set up the system of equations with the equation of the ellipse and the equation of the family of lines \( y - 4 = m(x - 4) \) for point P.

$$ \begin{cases} x^2 + 4y^2 = 20 \\ \\ y - 4 = m(x - 4) \end{cases} $$

Solve for \( y \) in the second equation and substitute it into the ellipse equation:

$$ x^2 + 4[m(x - 4) + 4]^2 = 20 $$

Expand and simplify:

$$ x^2 + 4[m(x - 4) + 4]^2 = 20 $$

$$ x^2 + 4[m^2(x - 4)^2 + 8m(x - 4) + 16] = 20 $$

$$ x^2 + 4m^2(x^2 - 8x + 16) + 32m(x - 4) + 64 = 20 $$

$$ x^2 + 4m^2x^2 - 32m^2x + 64m^2 + 32mx - 128m + 64 = 20 $$

$$ x^2(1 + 4m^2) + x(-32m^2 + 32m) + 64m^2 - 128m + 44 = 0 $$

Add the tangency condition \( \Delta = 0 \):

$$ \Delta = b^2 - 4ac = 0 $$

Where \( a = 1 + 4m^2 \), \( b = -32m^2 + 32m \), \( c = 64m^2 - 128m + 44 \):

$$ \Delta = (-32m^2 + 32m)^2 - 4(1 + 4m^2) \cdot (64m^2 - 128m + 44) = 0 $$

$$ \Delta = 1024m^4 - 2048m^3 + 1024m^2 - 1024m^4 + 2048m^3 - 960m^2 + 512m - 176 = 0 $$

$$ \Delta = 64m^2 + 512m - 176 = 0 $$

This is a quadratic equation in \( m \) that can be solved using the quadratic formula:

$$ m = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$

Where \( a = 64 \), \( b = 512 \), and \( c = -176 \):

$$ m = \frac{-512 \pm \sqrt{512^2 - 4 \cdot 64 \cdot (-176)}}{2 \cdot 64} $$

$$ m = \frac{-512 \pm \sqrt{262144 + 45056}}{128} $$

$$ m = \frac{-512 \pm \sqrt{307200}}{128} $$

$$ m = \frac{-512 \pm 554.256}{128} $$

Calculate the two values of \( m \):

$$ m_1 = \frac{-512 + 554.256}{128} = \frac{42.256}{128} \approx 0.33 $$

$$ m_2 = \frac{-512 - 554.256}{128} = \frac{-1066.256}{128} \approx -8.33 $$

Thus, the values of \( m \) that satisfy the tangency condition are:

$$ m \approx 0.33 \quad \text{and} \quad m \approx -8.33 $$

Now, with these values of \( m \), we can find the corresponding coordinates \( (x, y) \) using the line equation \( y = mx - 4m + 4 \):

• If \( m \approx 0.33 \), the equation of the tangent line is \( y = 0.33 \cdot x - 4 \cdot 0.33 + 4 \)
• If \( m \approx -8.33 \), the equation of the tangent line is \( y = -8.33 \cdot x - 4 \cdot (-8.33) + 4 \)

Both lines are tangent to the ellipse and pass through point P(4, 4).

And that's it.