How to Find the Equation of an Ellipse Given Two Points
To determine the equation of an ellipse centered at the origin that passes through two points (x1, y1) and (x2, y2) in the plane, you need to set up a system of two general ellipse equations, substituting the coordinates of the known points into each equation.
$$ \begin{cases} \frac{x_1^2}{a^2} + \frac{y_1^2}{b^2} = 1 \\ \\ \frac{x_2^2}{a^2} + \frac{y_2^2}{b^2} = 1 \end{cases} $$
Solving this system allows you to find the lengths of the semi-axes \(a\) and \(b\) for the ellipse equation.
A Practical Example
In this exercise, we need to find the equation of the ellipse that passes through the points \( A \left( \sqrt{3}, \frac{1}{2} \right) \) and \( B \left( -1, \frac{\sqrt{3}}{2} \right) \)
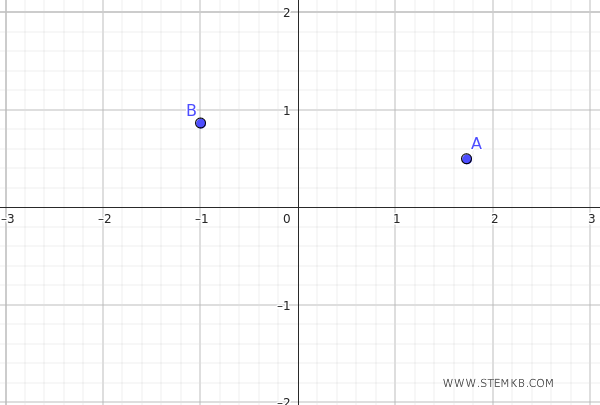
We start with the general form of the ellipse equation with its axes aligned with the Cartesian axes:
\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \]
Where \(a\) and \(b\) are the major and minor semi-axes, respectively.
We need to find \(a^2\) and \(b^2\) such that the ellipse passes through the given points.
We form an equation for each known point by substituting the coordinates \(x\) and \(y\) into the general ellipse equation.
For point \( A \left( \sqrt{3}, \frac{1}{2} \right) \):
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{(\sqrt{3})^2}{a^2} + \frac{\left( \frac{1}{2} \right)^2}{b^2} = 1 $$
$$ \frac{3}{a^2} + \frac{\frac{1}{4}}{b^2} = 1 $$
$$ \frac{3}{a^2} + \frac{1}{4b^2} = 1 $$
For point \( B \left( -1, \frac{\sqrt{3}}{2} \right) \):
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{(-1)^2}{a^2} + \frac{\left( \frac{\sqrt{3}}{2} \right)^2}{b^2} = 1 $$
$$ \frac{1}{a^2} + \frac{\frac{3}{4}}{b^2} = 1 $$
$$ \frac{1}{a^2} + \frac{3}{4b^2} = 1 $$
Now, we set up a system of two equations with two unknowns:
$$ \begin{cases} \frac{3}{a^2} + \frac{1}{4b^2} = 1 \\ \\ \frac{1}{a^2} + \frac{3}{4b^2} = 1 \end{cases} $$
To solve it, we can eliminate one of the unknowns. Multiply the first equation by 3:
$$ \begin{cases} 3 \left( \frac{3}{a^2} + \frac{1}{4b^2} \right) = 3 \\ \\ \frac{1}{a^2} + \frac{3}{4b^2} = 1 \end{cases} $$
$$ \begin{cases} \frac{9}{a^2} + \frac{3}{4b^2} = 3 \\ \\ \frac{1}{a^2} + \frac{3}{4b^2} = 1 \end{cases} $$
Now subtract the second equation from the first:
$$ \left( \frac{9}{a^2} + \frac{3}{4b^2} \right) - \left( \frac{1}{a^2} + \frac{3}{4b^2} \right) = 3 - 1 $$
$$ \require{cancel} \frac{9}{a^2} + \cancel{\frac{3}{4b^2}} - \frac{1}{a^2} - \cancel{\frac{3}{4b^2}} = 2 $$
$$ \frac{9}{a^2} - \frac{1}{a^2} = 2 $$
$$ \frac{8}{a^2} = 2 $$
$$ a^2 = 4 $$
$$ a = 2 $$
We have found the length of the horizontal semi-axis \(a\).
Now we substitute \( a^2 = 4 \) into one of the original system equations to find \(b\):
$$ \frac{1}{a^2} + \frac{3}{4b^2} = 1 $$
$$ \frac{1}{4} + \frac{3}{4b^2} = 1 $$
$$ \frac{3}{4b^2} = 1 - \frac{1}{4} $$
$$ \frac{3}{4b^2} = \frac{3}{4} $$
$$ 4 \cdot \frac{3}{4} = 3b^2 $$
$$ 3 = 3b^2 $$
Divide both sides by 3:
$$ b^2 = 1 $$
$$ \sqrt{b^2} = \sqrt{1} $$
$$ b = 1 $$
We have also found the length of the vertical semi-axis \(b\).
So, knowing that \( a=2 \) and \( b=1\), the equation of the ellipse is:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{2^2} + \frac{y^2}{1^2} = 1 $$
$$ \frac{x^2}{4} + y^2 = 1 $$
This equation passes through the points \( A \left( \sqrt{3}, \frac{1}{2} \right) \) and \( B \left( -1, \frac{\sqrt{3}}{2} \right) \)
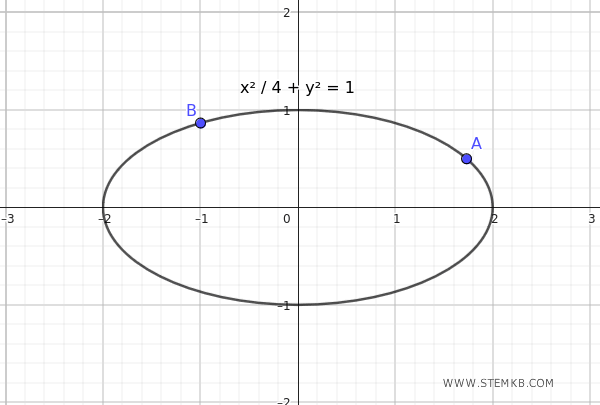
And there you have it.
