How to Determine the Equation of an Ellipse Given Its Eccentricity and a Vertex

To find the equation of an ellipse centered at the origin, expressed as $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$, and given a vertex $ V(x_v;y_v) $ and the eccentricity $ e $, we need to establish whether the major axis is horizontal or vertical.

• If the major axis is horizontal (a>b), use the eccentricity formula $ e = \frac{c}{a} $ and the relationship $ c^2 = a^2 - b^2 $.
• If the major axis is vertical (b>a), use the eccentricity formula $ e = \frac{c}{b} $ and the relationship $ c^2 = b^2 - a^2 $.

Knowing the vertex $ V(x_v;y_v) $ allows us to determine the length of either a semi-major or semi-minor axis.

If the problem doesn't specify the major axis, both possibilities must be considered.

A Practical Example

An ellipse centered at the origin has a vertex at \((-3,0)\) and \(e= \frac{\sqrt{7}}{3}\).

Knowing only a vertex doesn't reveal the major axis.

Therefore, we need to consider two scenarios: the major axis could be horizontal or vertical.

1] The Major Axis is Horizontal

In this scenario, the semi-major axis \(a\) is the larger one, where the foci of the ellipse are located.

For an ellipse centered at the origin with the vertex \((-3,0)\), the semi-major axis has a length of $ a=3 $.

Given \(a=3\), the eccentricity formula \(e\) is $ e=\frac{c}{a} $:

$$ e = \frac{c}{a} = \frac{\sqrt{7}}{3} $$

This means the distance from the center to the foci is $ c= \sqrt{7} $.

For a horizontal major axis, the relationship is \(c^2 = a^2 - b^2\).

$$ c^2 = a^2 - b^2 $$

Knowing $ a=3 $ and $ c= \sqrt{7} $:

$$ (\sqrt{7})^2 = 3^2 - b^2 $$

$$ 7 = 9 - b^2 $$

$$ b^2 = 9 - 7 $$

$$ b^2 = 2 $$

$$ b = \sqrt{2} $$

Now we have the lengths of the semi-major axis $ a = 3 $ and the semi-minor axis $ b = \sqrt{2} $.

Substituting \(a\) and \(b\) into the standard equation of the ellipse, we get:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

$$ \frac{x^2}{3^2} + \frac{y^2}{( \sqrt{2} )^2} = 1 $$

$$ \boxed{\frac{x^2}{9} + \frac{y^2}{2} = 1} $$

This is the equation of the ellipse with a vertex at \( (-3;0) \) and an eccentricity \( e= \frac{\sqrt{7}}{3} \) when the major axis is horizontal.

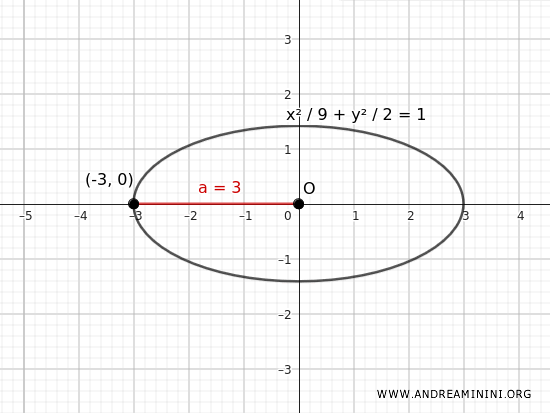
Note: With semi-axes $ a=3 $ and $ b = \sqrt{2} $, and the focal distance $ c= \sqrt{7} $, the eccentricity is $$ e = \frac{c}{a} = \frac{ \sqrt{7 }}{3 } $$

2] The Major Axis is Vertical

In this scenario, the semi-major axis \(b\) is the larger one, meaning the vertical axis is where the foci of the ellipse are located.

From the problem, we know the length of the semi-minor horizontal axis, which is $ a=3 $.

For a vertical major axis, the eccentricity formula is $ e = \frac{c}{b} $ and the relationship between the axes is $ c^2 = b^2 - a^2 $:

$$ e = \frac{c}{b} = \frac{\sqrt{7}}{3} $$

Where $ c^2 = b^2 - a^2 $, so $ c = \sqrt{b^2 - a^2} $:

$$ \frac{\sqrt{b^2 - a^2}}{b} = \frac{\sqrt{7}}{3} $$

Knowing the semi-minor horizontal axis is $ a=3 $:

$$ \frac{\sqrt{b^2 - 3^2}}{b} = \frac{\sqrt{7}}{3} $$

$$ \frac{\sqrt{b^2 - 9}}{b} = \frac{\sqrt{7}}{3} $$

$$ \sqrt{b^2 - 9} = \frac{\sqrt{7}}{3} b $$

Square both sides:

$$ (\sqrt{b^2 - 9})^2 = (\frac{\sqrt{7}}{3} b)^2 $$

$$ b^2 - 9 = \frac{7}{9} b^2 $$

$$ b^2 - \frac{7}{9} b^2 = 9 $$

$$ \frac{9b^2 - 7b^2}{9} = 9 $$

$$ \frac{2b^2}{9} = 9 $$

$$ b^2 = \frac{81}{2} $$

Taking the square root of both sides:

$$ \sqrt{b^2} = \sqrt{\frac{81}{2}} $$

$$ b = \frac{9}{\sqrt{2}} $$

Multiply and divide by $ \sqrt{2} $ to rationalize the denominator:

$$ b = \frac{9}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} $$

$$ b = \frac{9 \sqrt{2}}{2} $$

Now we know the lengths of the semi-minor axis $ a=3 $ and the semi-major axis $ b = \frac{9 \sqrt{2}}{2} $.

Substituting $ a $ and $ b $ into the equation of the ellipse:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

$$ \frac{x^2}{3^2} + \frac{y^2}{( \frac{9 \sqrt{2}}{2} )^2} = 1 $$

$$ \frac{x^2}{9} + \frac{y^2}{ \frac{81}{2} } = 1 $$

$$ \frac{x^2}{9} + y^2 \cdot \frac{2}{81} = 1 $$

$$ \boxed{ \frac{x^2}{9} + \frac{2y^2}{81} = 1 } $$

This is the equation of the ellipse with a vertex at \( (-3;0) \) and an eccentricity \( e= \frac{\sqrt{7}}{3} \) when the major axis is vertical.

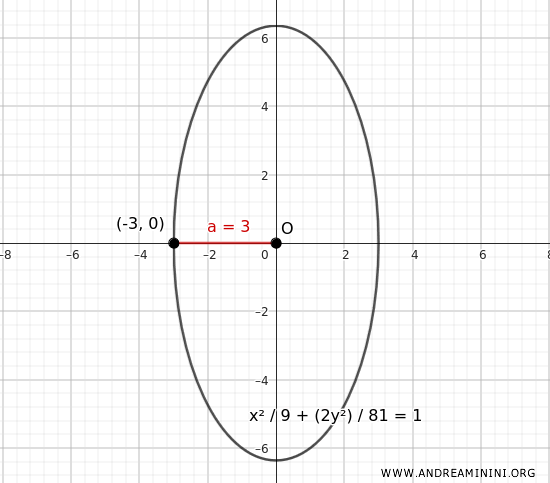
Note: With semi-axes $ a=3 $ and $ b= \frac{ 9 \sqrt{2} }{2 } $, the eccentricity is $$ e = \frac{c}{b} = \frac{c}{ \frac{ 9 \sqrt {2} }{2 } } $$ Knowing that $ c^2 = b^2 - a^2 $, then $ c = \sqrt{b^2 - a^2} $ $$ e = \frac{ \sqrt{b^2 - a^2}}{ \frac{ 9 \sqrt{2} }{2 } } $$ $$ e = \frac{ \sqrt{( \frac{ 9 \sqrt{2} }{2 } )^2 - 3^2}}{ \frac{ 9 \sqrt{2} }{2 } } $$ $$ e = \frac{ \sqrt{ \frac{ 81 }{2 } - 9 }}{ \frac{ 9 \sqrt{2} }{2 } } $$ $$ e = \frac{ \sqrt{ \frac{ 81 - 18 } {2 }}}{ \frac{ 9 \sqrt{2} }{2 } } $$ $$ e = \frac{ \sqrt{ \frac{ 63 }{2 }}}{ \frac{ 9 \sqrt{2} }{2 } } $$ $$ e = \frac{ \sqrt{63} }{\sqrt{2} } \cdot \frac{ 2 }{9 \sqrt{2} } $$ $$ e = \frac{ \sqrt{7 \cdot 3^2} }{2 } \cdot \frac{ 2 }{9 \sqrt{2} } $$ $$ e = \frac{ 3 \sqrt{7} }{ \sqrt{2} } \cdot \frac{\sqrt{2}}{ \sqrt{2}} \cdot \frac{ 2 }{9 \sqrt{2} } $$ $$ e = \frac{ 3 \sqrt{14} }{2 } \cdot \frac{ 2 }{9 \sqrt{2} } $$ $$ \require{cancel} e = \frac{ 3 \sqrt{14} }{ \cancel{2} } \cdot \frac{ \cancel{2} }{9 \sqrt{2} } $$ $$ e = \frac{ \sqrt{14} }{ 3 \sqrt{2} } $$ $$ e = \frac{1}{3} \cdot \frac{ \sqrt{14} }{ \sqrt{2} } $$ $$ e = \frac{1}{3} \cdot \sqrt{ \frac{14}{2}} $$ $$ e = \frac{1}{3} \cdot \sqrt{ 7 } $$ $$ e = \frac{ \sqrt{ 7 } }{3} $$

In conclusion, without additional information, both equations are valid solutions for the ellipse.

And so on.