Ellipse Tangent Line Formulas
The tangent line formulas help determine the equation of a tangent line at a point P(x0, y0) on the ellipse. $$ \frac{xx_0}{a^2} + \frac{yy_0}{b^2} = 1 $$
This formula can only be used if the point P(x0, y0) is on the ellipse. It does not work for points outside the ellipse.
If the ellipse is centered at a point other than the origin, the equation of the tangent line at a point P(x0, y0) on the ellipse can be calculated using the following splitting formula.
$$ A xx_0 + B yy_0 + C \frac{x+x_0}{2} + D \frac{y+y_0}{2} + E = 1 $$
In both cases, this is an application of the conic splitting formula to an ellipse.
Example
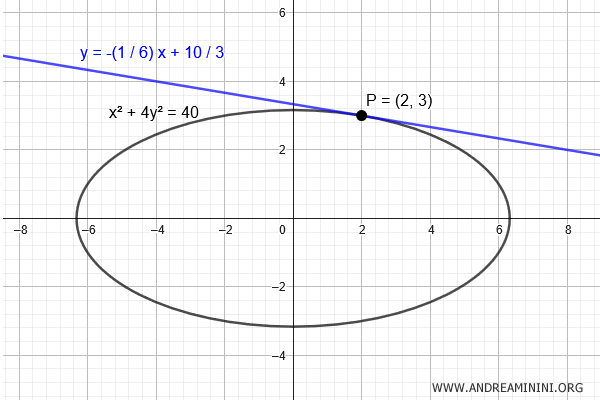
Consider the ellipse with the equation:
$$ x^2 + 4y^2 = 40 $$
We convert it to the standard form by dividing both sides by 40:
$$ \frac{x^2 + 4y^2}{40} = \frac{40}{40} $$
$$ \frac{x^2}{40} + \frac{y^2}{10} = 1 $$
Here, a2 = 40 and b2 = 10.
We need to find the equation of the tangent line to the ellipse at the point (2, 3).
$$ P(x_0, y_0) = (2, 3) $$
Using the tangent line formula with the coordinates x0 = 2 and y0 = 3:
$$ \frac{xx_0}{a^2} + \frac{yy_0}{b^2} = 1 $$
$$ \frac{x \cdot 2}{40} + \frac{y \cdot 3}{10} = 1 $$
$$ \frac{x}{20} + \frac{y \cdot 3}{10} = 1 $$
$$ y = \frac{10}{3} \cdot \left( 1 - \frac{x}{20} \right) $$
$$ y = -\frac{1}{6}x + \frac{10}{3} $$
This is the equation of the tangent line at the point P(2, 3) on the ellipse.
Example 2
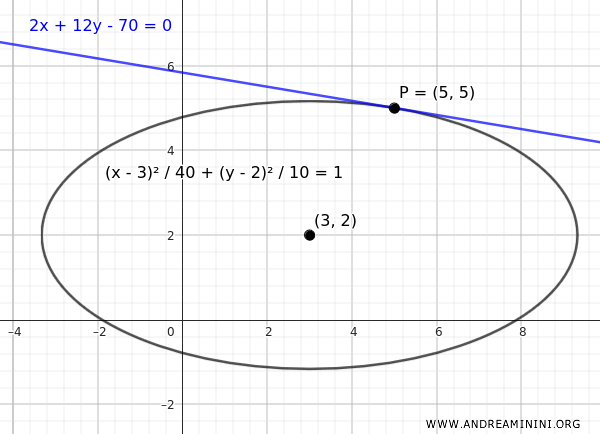
Consider an ellipse centered at the point P(3,2).
$$ \frac{ (x-3)^2}{40} + \frac{(y-2)^2}{10} = 1 $$
We transform the equation of the ellipse into the general form:
$$ \frac{x^2-6x+9}{40} + \frac{y^2-4y+4}{10} = 1 $$
$$ \frac{x^2-6x+9}{40} + \frac{4 \cdot (y^2-4y+4)}{40} = 1 $$
$$ \frac{x^2-6x+9 + 4 \cdot (y^2-4y+4)}{40} = 1 $$
$$ x^2-6x+9 + 4 \cdot (y^2-4y+4) = 40 $$
$$ x^2-6x+9 + 4y^2-16y+16 = 40 $$
$$ x^2 + 4y^2 -6x-16y + 16 + 9 - 40 = 0 $$
$$ x^2 + 4y^2 -6x-16y - 15 = 0 $$
Once we have the general form $ Ax^2 + By^2 + Cx + Dy + E = 0 $, we can find the equation of the tangent line at the point $ P(x_0, y_0) = (5,5) $ by substituting $ x^2 \rightarrow xx_0 $ and $ y^2 \rightarrow yy_0 $
$$ xx_0 + 4yy_0 -6x-16y - 15 = 0 $$
Next, we substitute $ x \rightarrow \frac{x+x_0}{2} $ and $ y \rightarrow \frac{y+y_0}{2} $
$$ xx_0 + 4yy_0 -6 ( \frac{x+x_0}{2} ) -16 ( \frac{y+y_0}{2} ) - 15 = 0 $$
$$ xx_0 + 4yy_0 -3 (x+x_0) -8 (y+y_0) - 15 = 0 $$
Finally, we substitute the coordinates of the point of tangency $ P(x_0, y_0) = (5,5) $, so $ x_0 = 5 $ and $ y_0 = 5 $
$$ x \cdot 5 + 4y \cdot 5 -3 (x+5) -8 (y+5) - 15 = 0 $$
$$ 5x + 20y -3x - 15 - 8y - 40 - 15 = 0 $$
$$ 2x + 12y - 70 = 0 $$
This is the equation of the tangent line to the ellipse at the point $ P(5,5) $
Proof
Let's start with the equation of the ellipse:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
Assume a tangent line to this ellipse passes through the point \((x_0, y_0)\) which lies on the ellipse, so:
$$ \frac{x_0^2}{a^2} + \frac{y_0^2}{b^2} = 1 $$
Consider the equation of a line passing through the point \((x_0, y_0)\):
$$ y = mx + c $$
Substitute this line equation into the ellipse's equation:
$$ \frac{x^2}{a^2} + \frac{(mx + c)^2}{b^2} = 1 $$
$$ \frac{x^2}{a^2} + \frac{m^2x^2 + 2mxc + c^2}{b^2} = 1 $$
Multiply by \(a^2b^2\) to clear the denominators:
$$ b^2x^2 + a^2m^2x^2 + 2a^2mxc + a^2c^2 = a^2b^2 $$
Rearrange the equation into quadratic form:
$$ (b^2 + a^2m^2)x^2 + 2a^2mxc + (a^2c^2 - a^2b^2) = 0 $$
For the line to be tangent to the ellipse, the discriminant of this quadratic equation must be zero. The discriminant \(\Delta\) for the quadratic equation \(Ax^2 + Bx + C = 0\) is given by:
$$ \Delta = B^2 - 4AC $$
Where \( A = b^2 + a^2m^2 \), \( B = 2a^2mc \), and \( C = a^2c^2 - a^2b^2 \)
Calculate the discriminant:
$$ \Delta = (2a^2mc)^2 - 4(b^2 + a^2m^2)(a^2c^2 - a^2b^2) $$
Expand and simplify:
$$ \Delta = 4a^4m^2c^2 - 4(b^2 + a^2m^2)(a^2c^2 - a^2b^2) $$
$$ \Delta = 4a^4m^2c^2 - 4[b^2a^2c^2 - b^2a^2b^2 + a^4m^2c^2 - a^4m^2b^2] $$
$$ \Delta = 4a^4m^2c^2 - 4b^2a^2c^2 + 4b^4a^2 - 4a^4m^2c^2 + 4a^4m^2b^2 $$
$$ \Delta = -4b^2a^2c^2 + 4b^4a^2 + 4a^4m^2b^2 $$
For the discriminant to be zero, \( \Delta = 0 \):
$$ -4b^2a^2c^2 + 4b^4a^2 + 4a^4m^2b^2 = 0 $$
Divide by \(4a^2\):
$$ -b^2c^2 + b^4 + a^2m^2b^2 = 0 $$
Simplify to obtain:
$$ b^2(b^2 + a^2m^2) = b^2c^2 $$
Divide by \(b^2\):
$$ b^2 + a^2m^2 = c^2 $$
$$ c^2 = b^2 + a^2m^2 $$
To find \(m\) and \(c\) in terms of \((x_0, y_0)\), we know \(y_0 = mx_0 + c\).
From this, we can express \(c\) as \( c = y_0 - mx_0 \)
Substitute \(c\) into the equation \(b^2 + a^2m^2 = c^2\):
$$ b^2 + a^2m^2 = (y_0 - mx_0)^2 $$
$$ b^2 + a^2m^2 = y_0^2 - 2y_0mx_0 + m^2x_0^2 $$
Rearrange to find \(m\):
$$ b^2 = y_0^2 - 2y_0mx_0 + m^2(x_0^2 - a^2) $$
Collect the \(m\) terms:
$$ b^2 = y_0^2 - 2y_0mx_0 + m^2(x_0^2 - a^2) $$
Now isolate \(m\):
$$ y_0^2 - 2y_0mx_0 + m^2(x_0^2 - a^2) = b^2 $$
Bring everything to the left to get a quadratic equation in \(m\):
$$ m^2(x_0^2 - a^2) - 2y_0mx_0 + (y_0^2 - b^2) = 0 $$
This is a quadratic equation in \(m\). We can solve it using the quadratic formula:
$$ m = \frac{-B \pm \sqrt{B^2 - 4AC}}{2A} $$
In this case, \( A = x_0^2 - a^2 \), \( B = -2y_0x_0 \), and \( C = y_0^2 - b^2 \)
For a tangent line, the discriminant must be zero:
$$ B^2 - 4AC = 0 $$
Thus:
$$ (-2y_0x_0)^2 - 4(x_0^2 - a^2)(y_0^2 - b^2) = 0 $$
$$ 4y_0^2x_0^2 - 4(x_0^2 - a^2)(y_0^2 - b^2) = 0 $$
$$ y_0^2x_0^2 = (x_0^2 - a^2)(y_0^2 - b^2) $$
Solving this equation, we find \(m\).
$$ y_0^2x_0^2 = (x_0^2 - a^2)(y_0^2 - b^2) $$
$$ y_0^2x_0^2 = x_0^2y_0^2 - x_0^2b^2 - y_0^2a^2 + a^2b^2 $$
$$ - x_0^2b^2 - y_0^2a^2 + a^2b^2 = 0 $$
$$ x_0^2b^2 + y_0^2a^2 = a^2b^2 $$
$$ \frac{x_0^2b^2}{a^2b^2} + \frac{y_0^2a^2}{a^2b^2} = \frac{a^2b^2}{a^2b^2} $$
$$ \frac{x_0^2}{a^2} + \frac{y_0^2}{b^2} = 1 $$
Since \((x_0, y_0)\) is a point on the ellipse and also a point on the tangent line, we can substitute \( x_0^2 = x_0 \cdot x \) and \( y_0^2 = y_0 \cdot y \).
$$ \frac{x_0 x}{a^2} + \frac{y_0 y}{b^2} = 1 $$
This equation satisfies the tangency condition for any point \((x_0, y_0)\) on the ellipse.
And so forth.
