How to Find the Equation of an Ellipse Given a Point and a Focus

To find the equation of an ellipse centered at the origin, given the coordinates of a focus $ F(c;0) $ or $ F(0;c) $ and a point $ P(x;y) $ on the ellipse, we need to set up a system of equations to determine the exact values of \( a \) and \( b \).

The first equation is obtained by substituting the coordinates of the point $ P(x;y) $ into the ellipse equation:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

The second equation depends on the orientation of the major axis, which can be deduced from the coordinates of the focus.

• If the major axis is horizontal, use the relationship between the semi-axes and the focus: $$ c = \sqrt{a^2 - b^2} $$
• If the major axis is vertical, use the relationship between the semi-axes and the focus: $$ c = \sqrt{b^2 - a^2} $$

Solving this system of equations allows us to determine the lengths of the semi-axes $ a $ and $ b $, and thus complete the equation of the ellipse.

How to determine the major axis?  This can be inferred from the coordinates of the focus. If the focus is at (c, 0), the major axis is horizontal (along the x-axis). Conversely, if the focus is at (0, c), the major axis is vertical (along the y-axis).

A Practical Example

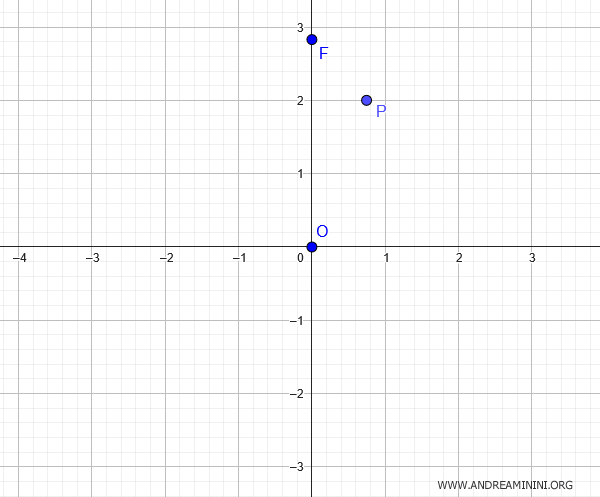
We need to find the equation of an ellipse centered at the origin with a focus at $ F(0; 2 \sqrt{2}) $ that passes through the point $ P( \frac{ \sqrt{5} }{3}; 2 ) $.

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

The ellipse has a vertical major axis because the focus $ F(0; 2 \sqrt{2}) $ lies on the y-axis.

When the major axis is vertical, the relationship between the semi-axes is:

$$ c = \sqrt{b^2 - a^2} $$

Given the coordinates of the focus $ F(0; 2 \sqrt{2}) $, where the y-coordinate is $ c = 2 \sqrt{2} $, we can write

$$ 2 \sqrt{2} = \sqrt{b^2 - a^2} $$

$$ (2 \sqrt{2})^2 = ( \sqrt{b^2 - a^2})^2 $$

$$ 4 \cdot 2 = b^2 - a^2 $$

$$ 8 = b^2 - a^2 $$

This is one of the equations in our system that will help us solve the problem.

The other equation is obtained by substituting the coordinates of the point $ P( \frac{ \sqrt{5} }{3}; 2 ) $ into the ellipse equation:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

$$ \frac{( \frac{ \sqrt{5} }{3} )^2}{a^2} + \frac{2^2}{b^2} = 1 $$

$$ \frac{ \frac{ 5 }{9} }{a^2} + \frac{4}{b^2} = 1 $$

$$ \frac{ 5 }{9a^2} + \frac{4}{b^2} = 1 $$

Now we have a system of equations:

$$ \begin{cases} b^2 - a^2 = 8 \\ \\ \frac{ 5 }{9a^2} + \frac{4}{b^2} = 1 \end{cases} $$

Substitute $ b^2 = 8 + a^2 $ into the second equation:

$$ \begin{cases} b^2 = 8 + a^2 \\ \\ \frac{ 5 }{9a^2} + \frac{4}{8 + a^2} = 1 \end{cases} $$

$$ \begin{cases} b^2 = 8 + a^2 \\ \\ \frac{ 5 }{9a^2} + \frac{4}{8 + a^2} - 1 = 0 \end{cases} $$

The second equation is a rational equation. To simplify, multiply each term by $ 9a^2(8 + a^2) $:

$$ \begin{cases} b^2 = 8 + a^2 \\ \\ \left( \frac{ 5 }{9a^2} + \frac{4}{8 + a^2} - 1 \right) \cdot [9a^2(8 + a^2)] = 0 \cdot [9a^2(8 + a^2)] \end{cases} $$

$$ \begin{cases} b^2 = 8 + a^2 \\ \\ 5 \cdot (8 + a^2) + 4 \cdot 9a^2 - 9a^2(8 + a^2) = 0 \end{cases} $$

$$ \begin{cases} b^2 = 8 + a^2 \\ \\ 40 + 5a^2 + 36a^2 - 72a^2 - 9a^4 = 0 \end{cases} $$

$$ \begin{cases} b^2 = 8 + a^2 \\ \\ 40 + a^2 (5 + 36 - 72) - 9a^4 = 0 \end{cases} $$

$$ \begin{cases} b^2 = 8 + a^2 \\ \\ 40 - 31a^2 - 9a^4 = 0 \end{cases} $$

$$ \begin{cases} b^2 = 8 + a^2 \\ \\ 9a^4 + 31a^2 - 40 = 0 \end{cases} $$

To solve the fourth-degree equation, introduce a variable $ k = a^2 $:

$$ 9a^4 + 31a^2 - 40 = 0 $$

$$ 9k^2 + 31k - 40 = 0 $$

Now we can solve for $ k $ using the quadratic formula:

$$ k = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$

Where \( a = 9 \), \( b = 31 \), and \( c = -40 \).

$$ k = \frac{-31 \pm \sqrt{31^2 - 4 \cdot 9 \cdot (-40)}}{2 \cdot 9} $$

$$ k = \frac{-31 \pm \sqrt{961 + 1440}}{18} $$

$$ k = \frac{-31 \pm \sqrt{2401}}{18} $$

$$ k = \frac{-31 \pm 49}{18} $$

Calculating the solutions for \( k \) (i.e., \( a^2 \)):

$$ k = \begin{cases} \frac{-31 - 49}{18} = - \frac{80}{18} = - \frac{40}{9} \\ \\ \frac{-31 + 49}{18} = \frac{18}{18} = 1 \end{cases} $$

The solutions for \( k \) (i.e., \( a^2 \)) from the quadratic equation are \( k = -\frac{40}{9} \) and \( k = 1 \).

Since \( k \) represents \( a^2 \), we only accept the positive solution \( k = 1 \).

$$ k = 1 $$

Knowing that the auxiliary variable is $ k = a^2 $:

$$ a^2 = 1 $$

Taking the square root of both sides:

$$ \sqrt{a^2} = \sqrt{1} $$

$$ a = 1 $$

After finding $ a = 1 $, substitute it into the first equation $ b^2 = 8 + a^2 $ to find $ b $:

$$ \begin{cases} b^2 = 8 + a^2 \\ \\ a = 1 \end{cases} $$

$$ \begin{cases} b^2 = 8 + 1^2 \\ \\ a = 1 \end{cases} $$

$$ \begin{cases} b^2 = 9 \\ \\ a = 1 \end{cases} $$

$$ \begin{cases} b = 3 \\ \\ a = 1 \end{cases} $$

The solutions for the system of equations are $ a = 1 $ and $ b = 3 $.

This leads us to the equation of the ellipse:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

$$ \frac{x^2}{1} + \frac{y^2}{3^2} = 1 $$

$$ x^2 + \frac{y^2}{9} = 1 $$

This is the final equation of the ellipse centered at the origin with the given data.

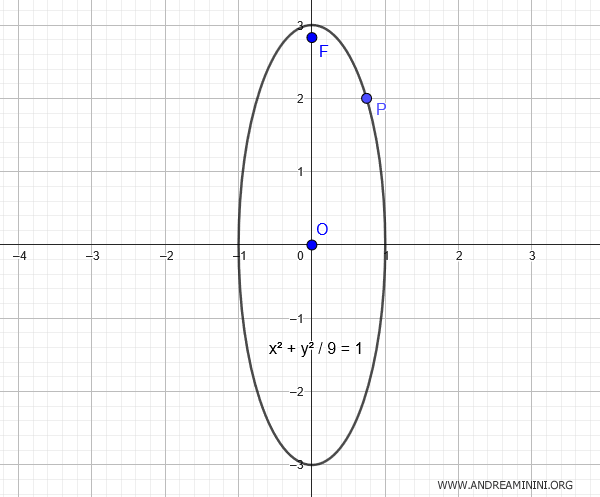
And that's how it's done.