Secant, Tangent, or External Line to an Ellipse

On a plane, a line can be secant, tangent, or external to an ellipse:

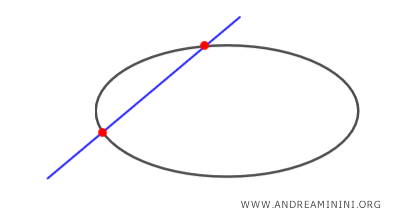
• It is secant if it intersects the ellipse at two points.
  
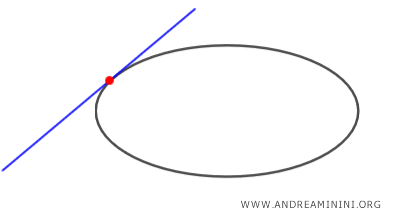
• It is tangent if it intersects the ellipse at exactly one point.
  
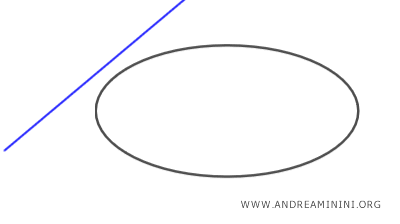
• It is external if it does not intersect the ellipse at any point.
  

To find the intersection points, you need to solve the system of equations composed of the line's equation and the ellipse's equation.

If the system has two distinct real solutions, the line is secant. If it has one real solution, it is tangent. If it has no real solutions, it is external.

A Practical Example

Consider the ellipse:

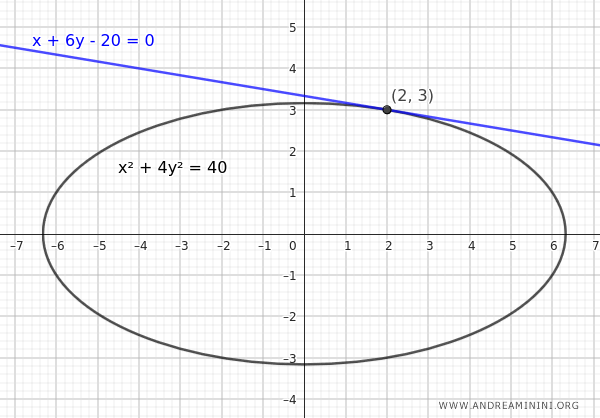
$$ x^2 + 4y^2 = 40 $$

and the line:

$$ x + 6y - 20 = 0 $$

We need to determine whether the line is secant, tangent, or external.

We set up the system of equations:

$$ \begin{cases} x^2 + 4y^2 = 40 \\ \\ x + 6y - 20 = 0 \end{cases} $$

We solve the system using the substitution method:

$$ \begin{cases} x^2 + 4y^2 = 40 \\ \\ x = 20 - 6y \end{cases} $$

$$ \begin{cases} (20 - 6y)^2 + 4y^2 = 40 \\ \\ x = 20 - 6y \end{cases} $$

$$ \begin{cases} 400 - 240y + 36y^2 + 4y^2 - 40 = 0 \\ \\ x = 20 - 6y \end{cases} $$

$$ \begin{cases} 40y^2 - 240y + 360 = 0 \\ \\ x = 20 - 6y \end{cases} $$

We simplify the first equation by dividing both sides by ten, and then by four:

$$ \begin{cases} 4y^2 - 24y + 36 = 0 \\ \\ x = 20 - 6y \end{cases} $$

$$ \begin{cases} y^2 - 6y + 9 = 0 \\ \\ x = 20 - 6y \end{cases} $$

The quadratic equation $ y^2 - 6y + 9 = 0 $ is the resolving equation of the system. The discriminant of this equation is:

$$ \Delta = b^2 - 4ac $$

$$ \Delta = (-6)^2 - 4 \cdot 1 \cdot 9 $$

$$ \Delta = 36 - 36 $$

$$ \Delta = 0 $$

Since the discriminant is zero, the system has a single solution, meaning the line is tangent to the ellipse.

Next, we solve the quadratic equation $ y^2 - 6y + 9 = 0 $ to find the value of y:

$$ y = \frac{-b \pm \sqrt{\Delta}}{2a} $$

$$ y = \frac{-(-6) \pm \sqrt{0}}{2 \cdot 1} $$

$$ y = \frac{6}{2} $$

$$ y = 3 $$

After finding y = 3, we substitute it back into the line's equation to find the value of x:

$$ \begin{cases} y = 3 \\ \\ x = 20 - 6 \cdot 3 \end{cases} $$

$$ \begin{cases} y = 3 \\ \\ x = 2 \end{cases} $$

Therefore, the point of tangency is at the coordinates (2, 3).

And that's how you determine if a line is secant, tangent, or external to an ellipse.