Equation of the Ellipse

The equation of the ellipse in a Cartesian coordinate system centered at the midpoint of the foci (the center of the ellipse) is: $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$ with $ a > 0 $ and $ b > 0 $

Here, x and y are the coordinates of any point P(x;y) on the ellipse.

• \(a\) is the semi-major axis, representing the distance from the center to the farthest point along the horizontal axis of the ellipse
• \(b\) is the semi-minor axis, representing the distance from the center to the nearest point along the vertical axis.

This is known as the "standard equation" of the ellipse and it applies whether the major axis is horizontal or vertical.

If the ellipse is centered at the point \((h, k)\) instead of the origin, the equation of the ellipse becomes:

$$ \frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1 $$

In general, an ellipse is defined as the set of points for which the sum of the distances from two fixed points, called the foci, is constant.

Note. In the ellipse equation, the coefficients must be greater than zero $ a > 0 $ and $ b > 0 $ as they represent the lengths of the semi-axes. Additionally, the constant term must be positive and equal to 1. If it is different from 1, an equivalent equation can be obtained by dividing all terms by that value.

The Axes, Vertices, Foci, and Eccentricity of the Ellipse

The relationship between \( a \) and \( b \) determines if the major axis is horizontal or vertical.

• If a > b, the major axis is horizontal (x-axis).
• If a < b, the major axis is vertical (y-axis).
• If a = b, the major and minor axes are equal, making the ellipse a circle.

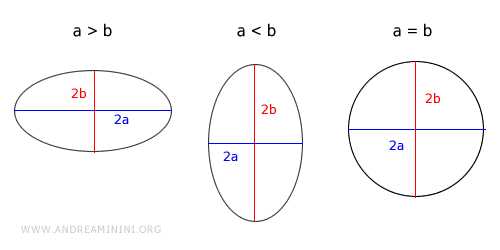
The coordinates of the foci of the ellipse vary depending on whether the major axis is horizontal (a > b) or vertical (a < b).

• If a > b: $$ F_1 ( - \sqrt{ a^2 - b^2 } ; 0 ) $$ $$ F_2 ( \sqrt{ a^2 - b^2 } ; 0 ) $$
• If a < b: $$ F_1 (0; - \sqrt{ b^2 - a^2 } ) $$ $$ F_2 ( 0; \sqrt{ b^2 - a^2 } ) $$

Where "a" and "b" are the lengths of the semi-axes of the ellipse.

The terms $ \sqrt{a^2 - b^2} $ and $ \sqrt{b^2 - a^2} $ measure the half of the focal distance (2c), which is the distance from each focus to the center (O), i.e., $ c = \overline{OF_1} = \overline{OF_2} $.

• If a > b: $$ c = \sqrt{a^2 - b^2} $$
• If a < b: $$ c = \sqrt{ b^2 - a^2 } $$

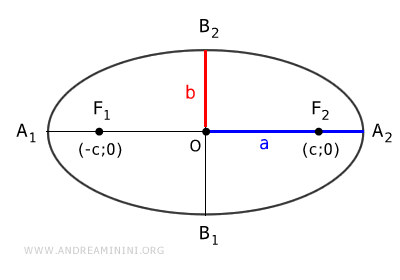
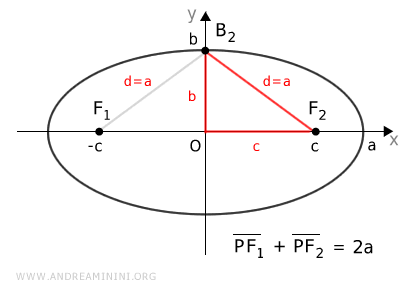
Proof. Let’s understand why $ c = \sqrt{ a^2 - b^2 } $. In an ellipse, the sum of the distances from any point P to the foci is constant: $$ \overline{PF_1} + \overline{PF_2} = k $$ Considering only the horizontal ellipse case (the same reasoning applies to a vertical ellipse), point $ A_2 $ is a vertex on the major axis.

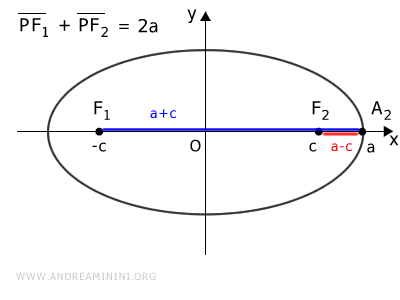
It's a point on the ellipse and the sum of the distances to the foci is constant. $$ \overline{A_2F_1} + \overline{A_2F_2} = k $$ Knowing the distances are $ \overline{A_2F_1} = a + c $ and $ \overline{A_2F_2} = a - c $, substituting these expressions into the equation: $$ (a + c) + (a - c) = k $$ $$ \require{cancel} a + \cancel{c} + a - \cancel{c} = k $$ $$ 2a = k $$ Thus, if the sum of the distances from the foci is $ k = 2a $ for point $ A_2 $, it must also be the same for any other point on the ellipse: $$ \overline{PF_1} + \overline{PF_2} = 2a $$ Now, considering the vertex $ B_2 $ on the minor axis:

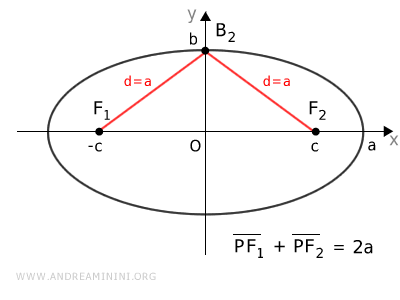
Measuring the sum of distances from $ B_2 $ to the foci: $$ \overline{B_2F_1} + \overline{B_2F_2} = 2a $$ Since $ B_2 $ lies on the symmetry axis, the distance to both foci is the same: $ \overline{B_2F_1} = \overline{B_2F_2} = a $. Thus, segment $ B_2 F_2 = a $. Once this is understood, the focal distance $ c = \overline{OF_2} $ can be found by applying the Pythagorean theorem to the triangle $OB_2F_2$: $ c = \sqrt{a^2 - b^2} $.

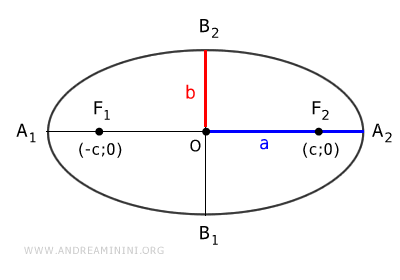
The vertices of the ellipse are the intersection points with the axes and are as follows:

$$ A_1 ( -a; 0 ) $$

$$ A_2 ( a; 0 ) $$

$$ B_1 ( 0; -b ) $$

$$ B_2 ( 0; b ) $$

The eccentricity (e) is a parameter that measures how much the ellipse deviates from being a circle, determined by the ratio of the focal distance (2c) to the length of the major axis (2a or 2b).

$$ e = \frac{\text{focal distance}}{\text{major axis length}} $$

Thus, the eccentricity formula changes depending on whether the ellipse is horizontal or vertical.

• If a > b, the eccentricity formula is: $$ e = \frac{c}{a} = \frac{\sqrt{a^2 - b^2}}{a} =  \sqrt{ 1 - \frac{b^2}{a^2}  } $$
• If a < b, the eccentricity formula is: $$ e = \frac{c}{b} = \frac{\sqrt{b^2 - a^2}}{b} = \sqrt{ 1 - \frac{a^2}{b^2}  } $$
• If a = b, either formula can be used.

The eccentricity is a parameter between 0 and 1.

$$ 0 \le e < 1 $$

When the eccentricity is zero (e = 0), the two foci coincide at a single point, and the ellipse degenerates into a circle.

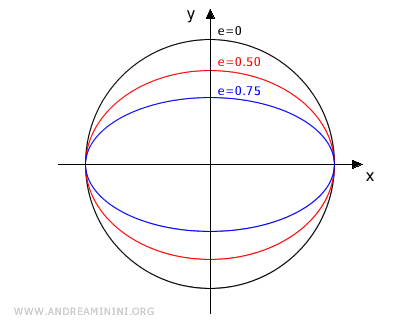
Conversely, the ellipse is very stretched along the major axis when the "e" parameter approaches 1.

Note.In the limiting case where the eccentricity is e = 1, the ellipse coincides with the major axis, and it is called a degenerate ellipse.

Every ellipse has two foci and two directrices, which are symmetrical and perpendicular to the focal axis.

If the focal axis lies along the \(x\)-axis, the directrices can be represented as:

$$ x = \pm \frac{a^2}{c} $$

When the focal axis aligns with the \(y\)-axis, the directrices are expressed as:

$$ y = \pm \frac{b^2}{c} $$

In general, for any conic section, given a point \( P(x;y) \) on the ellipse, the ratio between the distance \( \overline{PF} \) from the point to the focus and the distance \( \overline{PH} \) from the point to the directrix remains constant, corresponding to the ellipse's eccentricity:

$$ e = \frac{ \overline{PF} }{ \overline{PH} } $$

Here’s an example illustrating the directrices of an ellipse.

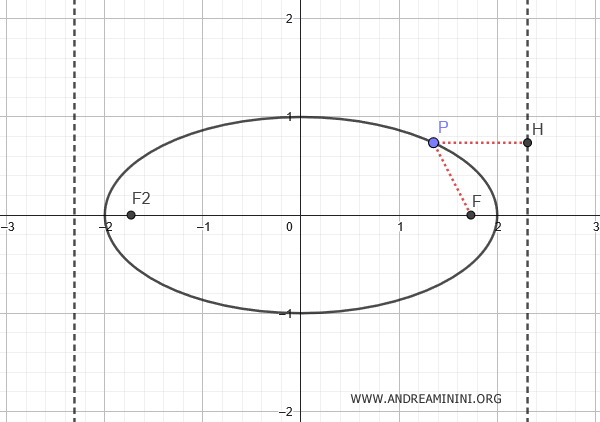
Proof: Consider an ellipse with its major axis along the x-axis. $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$ A directrix is a line perpendicular to the x-axis that passes through one of the foci, $ F(c, 0) $ $$ x = k $$ By definition, the ratio of the distance from any point on the ellipse to the focus and the distance from that point to the directrix is constant and equal to the eccentricity. $$ \frac{ \overline{PF} }{ \overline{PH} } = e $$ Here, the eccentricity is given by $ e = \frac{c}{a} $ $$ \frac{ \overline{PF} }{ \overline{PH} } = \frac{c}{a} $$ Now, let's take the point $ P $ at the vertex $ A(a,0) $ of the ellipse. The distance $ \overline{PF} = a-c $, while the distance $ \overline{PH} = k-a $ $$ \frac{ a-c }{ k-a } = \frac{c}{a} $$ $$ a \cdot (a-c)= c \cdot (k-a) $$ $$ \require{cancel} a^2 - \cancel{ac} = ck - \cancel{ac} $$ $$ a^2 = ck $$ $$ k = \frac{a^2}{c} $$ Since the other directrix is symmetric, the two directrices are located along the x-axis at the points $ (k, 0) $ and $ (-k, 0) $.

To find the intersections with the Cartesian axes, solve the system by setting x = 0 and then y = 0 in the ellipse equation.

$$ \begin{cases} \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \\ \\ x = 0 \end{cases} $$

When the ellipse is centered at the origin, the solution of the system is $ x = \pm a $, that is, the vertices $ A_1(-a;0) $ and $ A_2(a;0) $.

$$ \begin{cases} \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \\ \\ y = 0 \end{cases} $$

When the ellipse is centered at the origin, the solution of this system is $ y = \pm b $, that is, the vertices $ B_1(0;-b) $ and $ B_2(0;b) $.

 

A Practical Example

Consider the general equation of an ellipse centered at the origin with the main axes aligned with the Cartesian axes:

$$ \frac{x^2}{25} + \frac{y^2}{9} = 1 $$

In this case, the lengths of the axes are \( a = 5 \) and \( b = 3 \).

Since $ a > b $, the major axis is the horizontal x-axis.

The ellipse has its two main vertices on the x-axis at \( ( \pm a, 0 ) = ( \pm 5, 0 ) \) and the two minor vertices on the y-axis at \( (0, \pm b) = (0, \pm 3) \).

• The major axis is the distance between the two main vertices and is \( 2a = 2 \cdot 5 = 10 \).
• The minor axis is the distance between the two minor vertices and is \( 2b = 2 \cdot 3 = 6 \).

The center of the ellipse is at the origin of the axes.

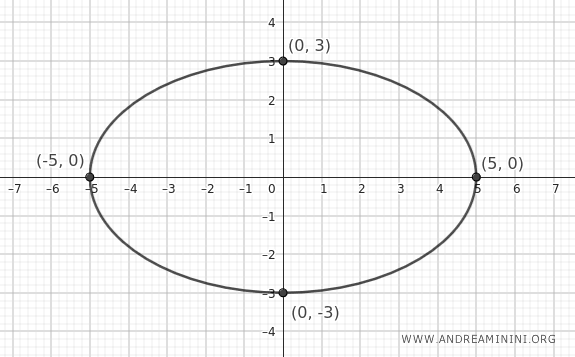
The distance of the foci from the center is determined by half the focal distance \( c \)

$$ c = \sqrt{a^2 - b^2} $$

$$ c = \sqrt{5^2 - 3^2} = \sqrt{25 - 9} = \sqrt{16} = 4 $$

Thus, the foci are located at \( ( \pm c, 0 ) \), or the points \( ( \pm 4, 0 ) \).

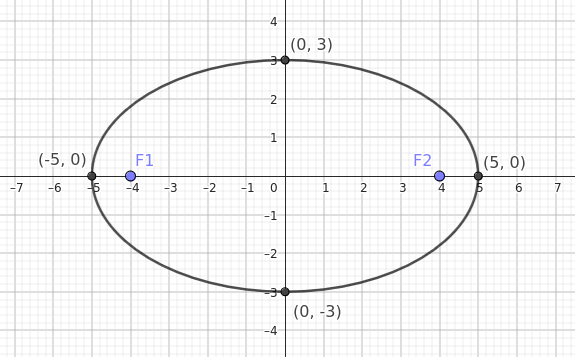
The eccentricity \( e \) of the ellipse is given by \( e = \frac{c}{a} \).

$$ e = \frac{4}{5} = 0.8 $$

The focal axis of the ellipse is the x-axis. Therefore, the directrices of the ellipse are given by:

$$ x = \pm \frac{a^2}{c} = \pm \frac{25}{4} \approx \pm 6.25 $$

For any point $ P(x;y) $ on the ellipse, the ratio of the distances $ \frac{ \overline{PF} }{ \overline{PH} } = e $ remains constant, and this constant is the eccentricity of the ellipse.

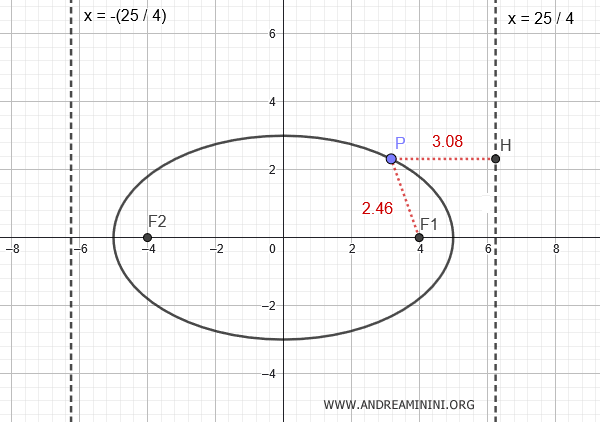
For instance, at point $ P $, the distance from the point to the focus is $ \overline{PF} = 2.46 $, while the distance from the point to the directrix is $ \overline{PH} = 3.08 $.

The ratio between these two distances equals the eccentricity of the ellipse:

$$ \frac{ \overline{PF} }{ \overline{PH} } = \frac{2.46}{3.08} = 0.8 = e $$

This relationship holds true for any point on the ellipse.

This completes the study of the ellipse.

Additional Notes

Some observations and side notes on the ellipse equation:

• The ellipse equation is not a function because for each value of the independent variable x, except for the vertices on the horizontal axis (A₁ and A₂), it yields two values of the dependent variable y. $$ y^2 = b^2 \cdot (1 - \frac{x^2}{a^2}) $$ $$ \sqrt{y^2} = \sqrt{ \frac{b^2}{a^2} \cdot (a^2 - x^2)} $$ $$ y = \pm \frac{b^2}{a^2} \cdot \sqrt{a^2 - x^2} $$ The ellipse equation can be considered as the union of two functions: $$ y = \frac{b^2}{a^2} \cdot \sqrt{a^2 - x^2} $$ and $$ y = - \frac{b^2}{a^2} \cdot \sqrt{a^2 - x^2} $$

And so on.