How to Determine the Equation of an Ellipse Given a Focus and a Vertex
To determine the equation of an ellipse centered at the origin given a vertex and a focus, you can find the length of the missing semi-axis using the Pythagorean theorem.
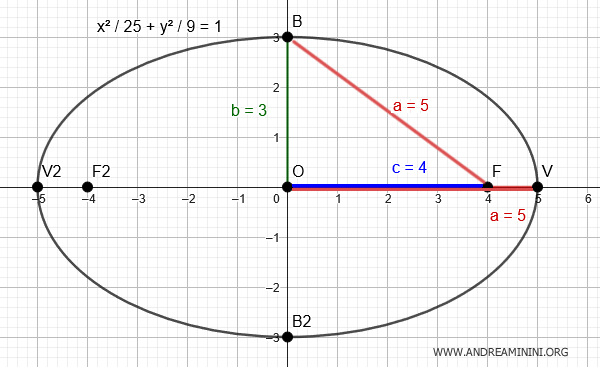
An ellipse forms a triangle between the origin, a focus, and a vertex (OF2B2).
In this triangle, one leg $ c $ is the distance from the focus to the center, the other leg $ b $ is the semi-minor axis of the ellipse, and the hypotenuse $ d=a $ is equal to the semi-major axis $ a $ of the ellipse.
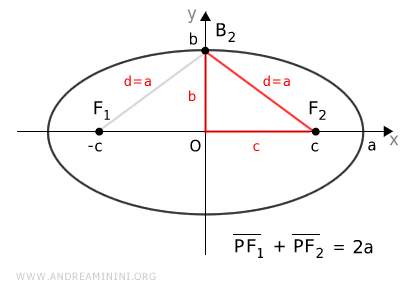
Therefore, to find the length of the missing semi-axis of the ellipse, simply use the Pythagorean theorem.
Note: Knowing the center is crucial for solving the problem. Knowing only the vertex and the focus without the center is not sufficient. In this example, we assume the ellipse is centered at the origin $ O(0;0) $.
A Practical Example
Consider an ellipse centered at the origin \((0,0)\), with a vertex at \( V(5,0)\) and a focus at \( F(4,0)\).
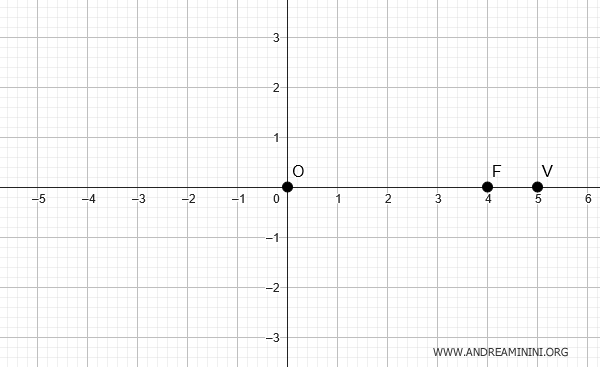
We need to determine the equation of the ellipse.
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
Where $ a $ is the length of the semi-major axis along the x-axis and $ b $ is the length of the semi-minor axis along the y-axis.
The focus \( F(4,0)\) and the vertex \( V(5,0)\) are on the x-axis. This means that the major axis of the ellipse is horizontal.
Additionally, the length of the horizontal semi-axis $ a $ is the distance between the center \((0,0)\) and the vertex \( V(5,0)\)
$$ a = \sqrt{ (x_v-x_o)^2 + (y_v-y_o)^2 } $$
$$ a = \sqrt{ (5-0)^2 + (0-0)^2 } $$
$$ a = \sqrt{ 25 } $$
$$ a = 5 $$
Therefore, the length of the horizontal semi-axis is $ a = 5 $
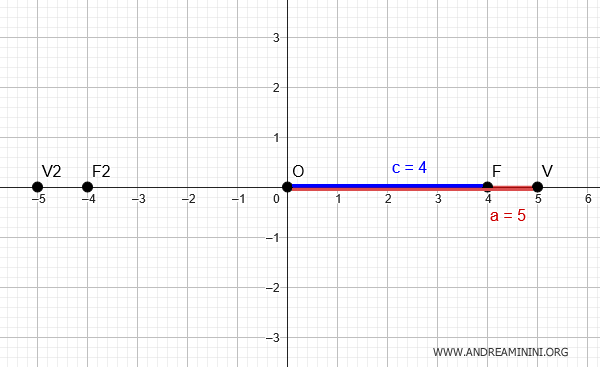
Additionally, the distance from the center to each focus is \(c = 4\).
Note: One of the foci is at \((4,0)\), which implies the other focus is at \((-4,0)\) since the foci are symmetric about the origin. Similarly, if one vertex is \((5,0)\), the other vertex must be \((-5,0)\) as the vertices are also symmetric about the origin.
Knowing that the length of the major semi-axis $ a $ is equal to the distance between the focus \(F(4,0)\) and the vertex $ B $ on the minor semi-axis, to find the length of the minor semi-axis $ b $, we apply the Pythagorean theorem.
$$ c^2 = a^2 - b^2 $$
Given that $ c = 4 $ and $ a = 5 $
$$ 4^2 = 5^2 - b^2 $$
$$ 16 = 25 - b^2 $$
$$ b^2 = 25 - 16 $$
$$ b^2 = 9 $$
$$ b = 3 $$
This means the vertical semi-axis measures $ b = 3 $, and the other vertices are located at $ B( 0;3 ) $ and $ B_2( 0;-3 ) $
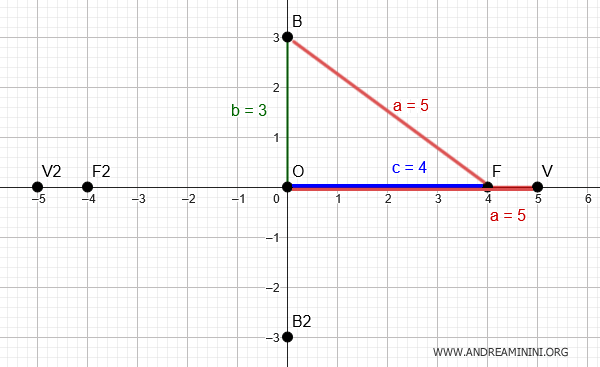
Now we have all the values needed to write the equation of the ellipse.
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{25} + \frac{y^2}{9} = 1 $$
Here is the graphical representation of the equation:
And that's it!
