How to Find the Equation of an Ellipse Given a Focus and a Semi-Axis

To find the equation of an ellipse centered at the origin O(0,0) with a known focus F(x_f,y_f) and the length of a semi-axis, we can use the Pythagorean theorem.

A Practical Example

Let's consider an ellipse centered at the origin $ O(0,0) $ with a known focus $ F(4,0) $ and a vertical semi-axis length of $ b=3 $.

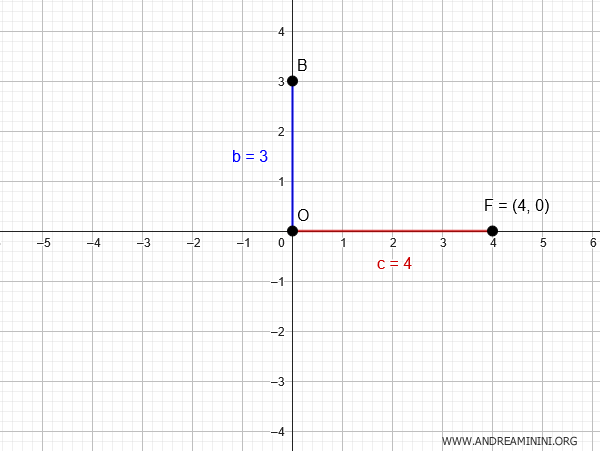
The distance between the focus and the center gives us the focal distance $ c = 4 $.

The equation of an ellipse centered at the origin is:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

We already know the length of the vertical semi-axis $ b=3 $. To complete the equation, we need to find the length of the horizontal semi-axis.

Knowing that the length of the horizontal semi-axis $ a $ is related to the distance between the focus and the vertex B(0,3) of the vertical semi-axis, we can determine it using the Pythagorean theorem.

$$ a^2 = b^2 + c^2 $$

Substituting $ b=3 $ and $ c=4 $, we get:

$$ a^2 = 3^2 + 4^2 $$

$$ a^2 = 9 + 16 $$

$$ a^2 = 25 $$

$$ a = 5 $$

Therefore, the vertices on the horizontal semi-axis are $ A(5,0) $ and $ A_2(-5,0) $, being symmetric with respect to the center $ O(0,0) $ of the ellipse.

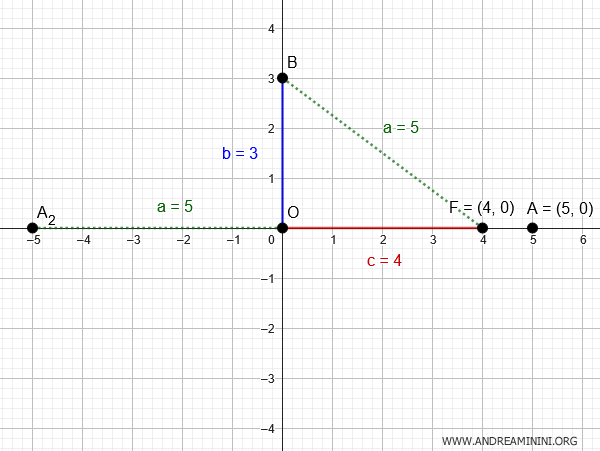
Now that we have all the necessary data $ a=5 $ and $ b=3 $, we can write the equation of the ellipse:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

$$ \frac{x^2}{5^2} + \frac{y^2}{3^2} = 1 $$

$$ \frac{x^2}{25} + \frac{y^2}{9} = 1 $$

Here's the graphical representation of the equation:

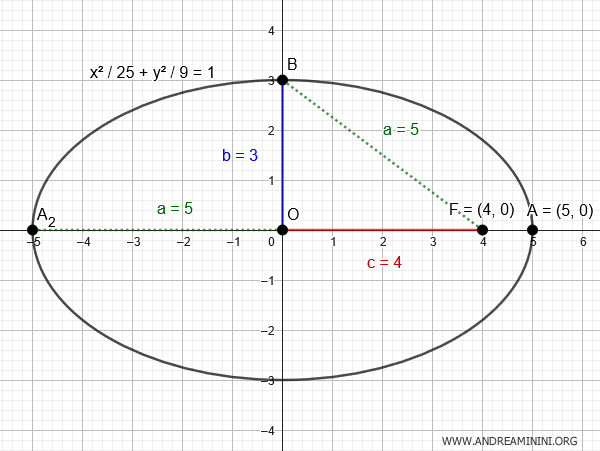
And that's how it's done.