Method of Completing the Square for an Ellipse
The completing the square method allows us to determine the characteristics of an ellipse by analyzing its general equation $$ Ax^2 + By^2 + Cx + Dy + E = 0 $$. By grouping the x and y terms, we can form binomials squared in each parenthesis, thus converting the equation into the standard form of an ellipse: $$ \frac{(x-x_0)^2}{a^2} + \frac{(y-y_0)^2}{b^2} = 1 $$ where $ (x_0;y_0) $ is the center of the ellipse.
A Practical Example
Let's consider the general equation of an ellipse:
$$ 25x^2 + 9y^2 - 100x - 18y - 116 = 0 $$
We need to transform this equation into the standard form $$ \frac{(x-x_0)^2}{a^2} + \frac{(y-y_0)^2}{b^2} = 1 $$. First, we move the constant term to the right side of the equation:
$$ 25x^2 + 9y^2 - 100x - 18y = 116 $$
Next, we group the x and y terms:
$$ 25(x^2 - 4x) + 9(y^2 - 2y) = 116 $$
Now, let's apply the completing the square method. For the x terms, we add 4·25 to both sides of the equation:
$$ 25(x^2 - 4x) + 4 \cdot 25 + 9(y^2 - 2y) = 116 + 4 \cdot 25 $$
$$ 25(x^2 - 4x + 4) + 9(y^2 - 2y) = 116 + 100 $$
$$ 25(x - 2)^2 + 9(y^2 - 2y) = 216 $$
Next, for the y terms, we add 1·9 to both sides of the equation:
$$ 25(x - 2)^2 + 9(y^2 - 2y) + 1 \cdot 9 = 216 + 1 \cdot 9 $$
$$ 25(x - 2)^2 + 9(y^2 - 2y + 1) = 216 + 9 $$
$$ 25(x - 2)^2 + 9(y - 1)^2 = 225 $$
Now, we divide both sides of the equation by 225:
$$ \frac{ 25(x - 2)^2 }{225} + \frac{ 9(y - 1)^2 }{ 225 } = \frac{225}{225} $$
$$ \frac{ 25(x - 2)^2 }{225} + \frac{ 9(y - 1)^2 }{ 225 } = 1 $$
$$ \frac{ (x - 2)^2 }{ \frac{225}{25} } + \frac{ (y - 1)^2 }{ \frac{225}{9} } = 1 $$
$$ \frac{ (x - 2)^2 }{ 9 } + \frac{ (y - 1)^2 }{ 25 } = 1 $$
The final result is the standard form of the ellipse equation.
From this form, we can immediately see that the ellipse is centered at (2,1).
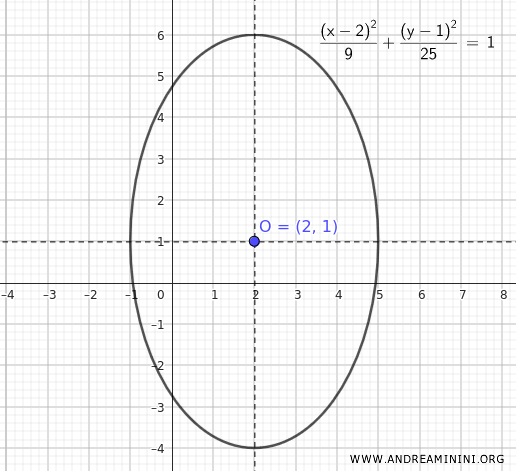
Therefore, the axes of symmetry of the ellipse are $ x=2 $ and $ y=1 $.
Moreover, the terms $ a^2=9 $ and $ b^2=25 $ allow us to calculate the lengths of the semi-axes $ a=3 $ and $ b=5 $.
In this case, since $ b > a $, the major semi-axis of the ellipse is vertical, parallel to the y-axis.
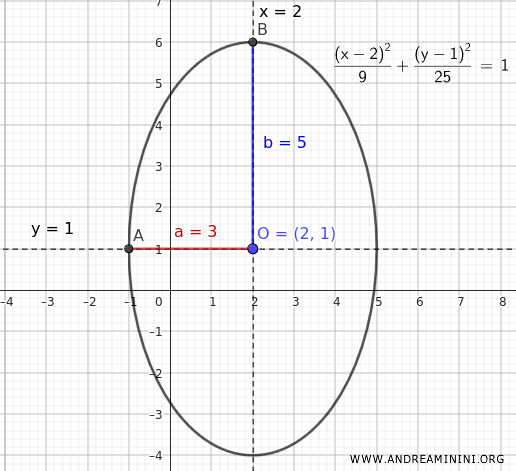
Knowing the center (2,1) and the lengths of the semi-axes, we can easily calculate the vertices:
$$ A ( 2 \pm a, 1 ) = (2 \pm 3, 1) = \begin{cases} A_1 (-1,1) \\ \\ A_2 (5,1) \end{cases} $$
$$ B = (2, 1 \pm b) = (2, 1 \pm 5) = \begin{cases} B_1 (2,-4) \\ \\ B_2 (2,6) \end{cases} $$
Finally, knowing $ a = 3 $ and $ b = 5 $, we can calculate the position of the foci on the vertical axis, using the relationship $ c^2 = b^2 - a^2 $:
$$ c^2 = b^2 - a^2 $$
$$ c^2 = 5^2 - 3^2 $$
$$ c^2 = 25 - 9 $$
$$ c^2 = 16 $$
$$ \sqrt{c^2} = \sqrt{16} $$
$$ c = 4 $$
Thus, along the line y=1, the foci are at the coordinates:
$$ F (2, 1 \pm 4) = \begin{cases} F_1 (2,-3) \\ \\ F_2 (2,5) \end{cases} $$
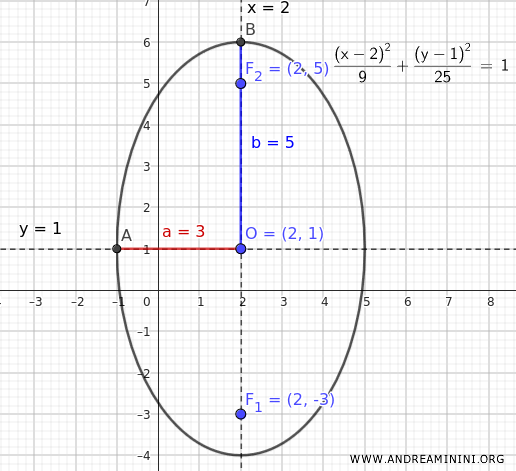
And that's it!
