How to Determine the Equation of an Ellipse Given Its Eccentricity and a Focus
To determine the equation of an ellipse centered at the origin, given the eccentricity \( e = \frac{2 \sqrt{5}}{5} \) and the coordinates of a focus, follow these steps:
- The focus helps identify the major axis of the ellipse.
- If the major axis is horizontal (a > b), the formula for eccentricity is $$ e = \frac{c}{a} $$, otherwise, if it's vertical (a < b), the formula is $$ e = \frac{c}{b} $$.
- The formula for eccentricity allows us to find the length of the semi-major axis.
- Once the length of the semi-major axis is found, calculate the semi-minor axis using the relation $ c = \sqrt{a^2 - b^2} $ if the major axis is horizontal (a > b) or $ c = \sqrt{b^2 - a^2} $ if the major axis is vertical (a < b).
A Practical Example
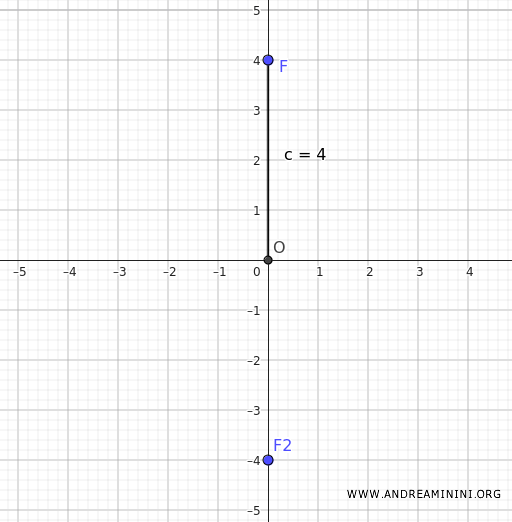
Consider an ellipse centered at the origin, with eccentricity \( e = \frac{2 \sqrt{5}}{5} \) and a focus at \((0, 4)\).
The foci of an ellipse centered at the origin are symmetric with respect to the origin. So, if one focus is at \((0, 4)\), the other focus will be at \((0, -4)\).

Knowing that the foci are always on the major axis, we deduce that in this ellipse, the major axis is vertical.
The distance between the two foci \(2c\) is equal to the distance between the points \((0, 4)\) and \((0, -4)\), which is 8.
$$ 2c = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$
$$ 2c = \sqrt{(0 - 0)^2 + (4 - (-4))^2} $$
$$ 2c = \sqrt{8} $$
Therefore, if \(2c = 8\), then the distance from the center to a focus is half of that, \(c = 4\).
$$ c = 4 $$
When the major axis is vertical, the eccentricity \(e\) is defined as \(e = \frac{c}{b}\), where \(b\) is the semi-major axis.
$$ e = \frac{c}{b} $$
Given \(e = \frac{2 \sqrt{5}}{5}\) and \(c = 4\), we can calculate \(b\):
$$ \frac{2 \sqrt{5}}{5} = \frac{c}{b} $$
$$ \frac{2 \sqrt{5}}{5} = \frac{4}{b} $$
$$ b = \frac{4 \cdot 5}{2 \sqrt{5}} $$
$$ b = \frac{20}{2 \sqrt{5}} $$
$$ b = \frac{10}{\sqrt{5}} $$
$$ b = 2\sqrt{5} $$
Now, let's find the semi-minor axis \(a\), knowing that for ellipses with a vertical major axis (b > a), the relation is:
$$ c = \sqrt{b^2 - a^2} $$
Where \(b = 2\sqrt{5}\) and \(c = 4\):
$$ 4 = \sqrt{(2\sqrt{5})^2 - a^2} $$
$$ 4 = \sqrt{4 \cdot 5 - a^2} $$
$$ 4 = \sqrt{20 - a^2} $$
Squaring both sides of the equation:
$$ 4^2 = (\sqrt{20 - a^2})^2 $$
$$ 16 = 20 - a^2 $$
$$ a^2 = 20 - 16 $$
$$ a^2 = 4 $$
$$ \sqrt{a^2} = \sqrt{4} $$
$$ a = 2 $$
So, the horizontal semi-minor axis is 2.
Given \(a = 2\) and \(b = 2\sqrt{5}\), we can write the equation of the ellipse:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{2^2} + \frac{y^2}{(2\sqrt{5})^2} = 1 $$
$$ \frac{x^2}{4} + \frac{y^2}{20} = 1 $$
Therefore, the equation of the ellipse is:
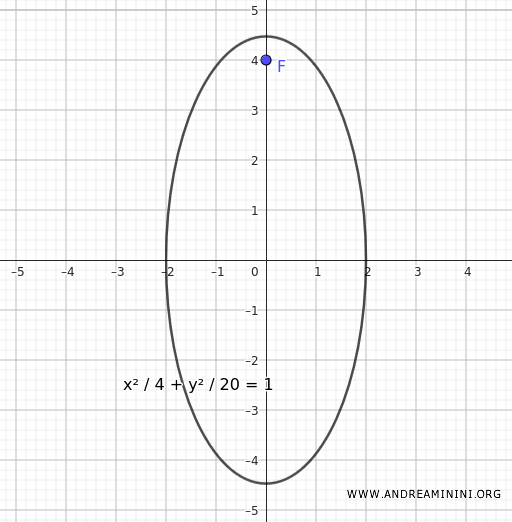
$$ \frac{x^2}{4} + \frac{y^2}{20} = 1 $$
Here is the graphical representation:
And so on.
