Focal Radius in a Conic Section

The focal radius in a conic section is the line segment that connects any point $ P $ on the curve to one of its foci $ F $.

Conic sections include familiar curves like ellipses, parabolas, and hyperbolas. These curves, also called "conics," are formed by slicing a cone with a plane in different ways.

To better understand the concept of the focal radius, let's look at the different types of conic sections:

• Parabola
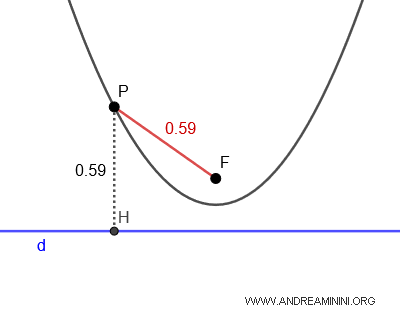
  A parabola has a single focus $ F $. Therefore, for any point $ P $ on the parabola, there is only one focal radius $ \overline{PF} $. Additionally, any point $ P $ on the parabola is equidistant from the focus $ F $ and the directrix (d).
  
• Ellipse
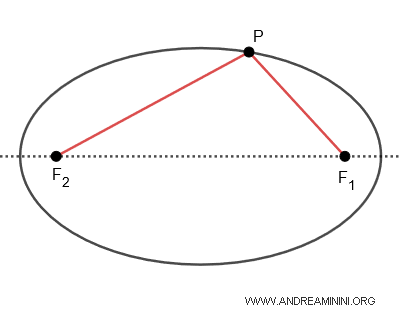
  An ellipse has two foci, $ F_1 $ and $ F_2 $. Therefore, for each point $ P $ on the ellipse, there are two focal radii, \(PF_1\) and \(PF_2\). Moreover, in an ellipse, the sum of the distances from any point $ P $ on the ellipse to each of the two foci is constant: $ \overline{PF_1} + \overline{PF_2} = k  $.
  
• Hyperbola
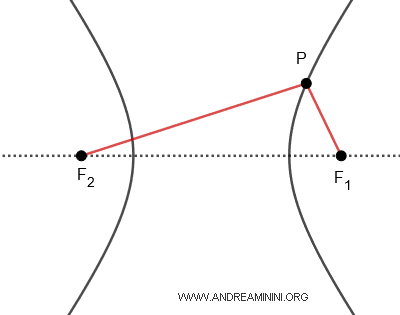
  A hyperbola also has two foci, $ F_1 $ and $ F_2 $. Thus, for any point \(P\) on the curve, there are two focal radii, $ \overline{PF_1} $ and $ \overline{PF_2} $. Additionally, in a hyperbola, the difference between the distances from any point $ P $ on the curve to the two foci is constant: $ \overline{PF_1} - \overline{PF_2} = k  $.
  

In all cases, the focal radius is the distance between a specific point on a conic section (whether it’s an ellipse, parabola, or hyperbola) and one of its foci.

The focal radius is a key concept because it connects points on a conic section to its foci, helping to define the optical properties of these curves. It also has various practical applications.

For instance, in an ellipse, any light or sound wave originating from one focus will be reflected so that it passes through the other focus. This principle is used in a range of optical and acoustic devices. In a parabola, all waves arriving parallel to the axis of symmetry are focused precisely at the focus, which explains the use of parabolic shapes in satellite dishes and headlights.

And so on.