Polar Line and Tangents

The polar line of tangents is a line, r, associated with a point P outside a conic (e.g., a circle). The points of contact, A and B, between r and the conic are also the points of contact of the tangents to the conic that pass through P.

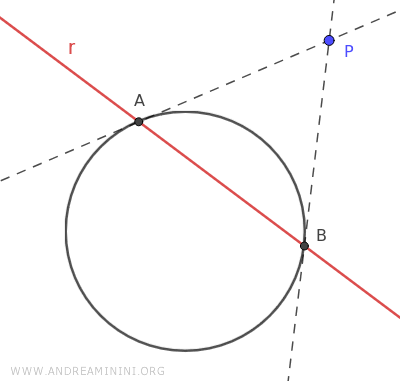
To better understand this concept, consider a circle \(\mathcal{C}\) and a point \(P\) outside of it.

Draw the tangents to the circle that pass through the external point P.

Since P is outside the circle, there are two tangents and therefore two points of contact with the circle.

The polar line associated with P is the (red) line that passes through the two points of tangency, A and B, on the circle.

To find the equation of the polar line for a conic $ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $ and a point $ P(x_0, y_0) $, you can use the following formula:

$$ Axx_0 + B\left(\frac{xy_0 + yx_0}{2}\right) + Cyy_0 + Dx + Ey + F = 0 $$

Note: The polar line of tangents represents a link between a conic and any external point through the geometric locus of the tangents to the conic that pass through that point.

Practical Example

As an example, consider a circle and a point \( Q(6, 8) \) outside the circle.

$$ x^2 + y^2 - 25 = 0 $$

$$ Q(6,8) $$

Using the formula:

$$ Axx_0 + B\left(\frac{xy_0 + yx_0}{2}\right) + Cyy_0 + Dx + Ey + F = 0 $$

Substitute the conic coefficients: A=1, B=0, C=1, D=0, E=0, F=-25

$$ 1 \cdot xx_0 + 0 \cdot \left(\frac{xy_0 + yx_0}{2}\right) + 1 \cdot yy_0 + 0 \cdot x + 0 \cdot y - 25 = 0 $$

$$ xx_0 + yy_0 - 25 = 0 $$

Explanation: A conic is generally represented by the equation $$ Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0 $$. In this case, it is a circle $$ x^2 + y^2 = 25 $$. So, the coefficients are A=1, B=0, C=1, D=0, E=0, F=-25.

The coordinates of the external point Q(6,8) are x₀=6 and y₀=8.

$$ x \cdot 6 + y \cdot 8 - 25 = 0 $$

Thus, we find the equation of the polar line:

$$ 6x + 8y - 25 = 0 $$

This line represents the polar line of the point \( Q(6, 8) \) with respect to the circle \( x^2 + y^2 = 25 \).

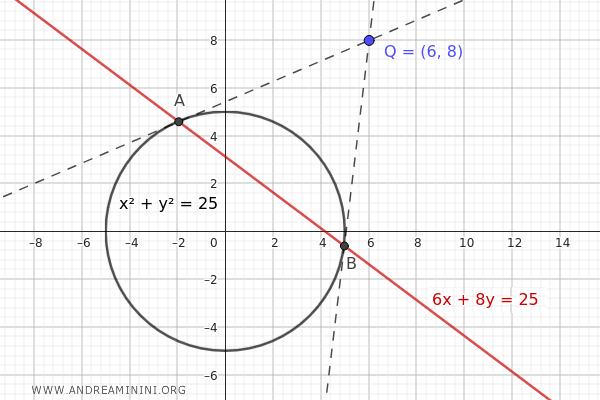
As shown in the graph, the two intersection points A and B of the polar line with the circle coincide with the points of contact of the two tangent lines passing through the external point \( Q(6, 8) \).

Observations

Some useful observations about the polar line:

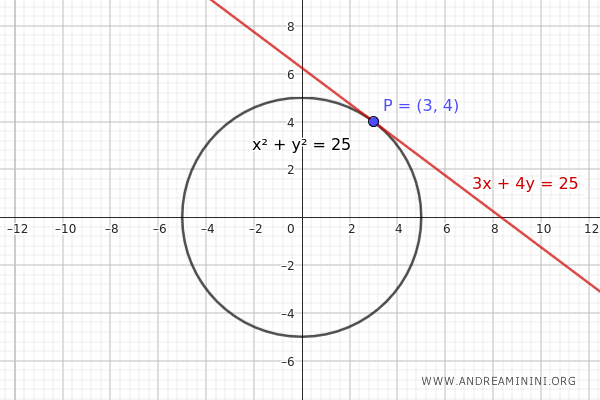
• If point P is on the circle, the polar line coincides with the tangent at P
  When a point P is on a conic, such as a circle, its polar line coincides with the tangent to the conic at that point.

  Example: Consider a circle centered at the origin with a radius r=25. $$ x^2 + y^2 = 25 $$ Now, take the point \(P(3, 4)\) which is exactly on the circle. Applying the formula: $$ Axx_0 + B\left(\frac{xy_0 + yx_0}{2}\right) + Cyy_0 + Dx + Ey + F = 0 $$ In this case, the coefficients are A=1, B=0, C=1, D=0, E=0, F=-25 $$ xx_0 + yy_0 - 25 = 0 $$ The coordinates of point P(3,4) are x₀=3 and y₀=4. $$ 3x + 4y - 25 = 0 $$ This equation represents a tangent line to the circle passing through point P(3,4).
  

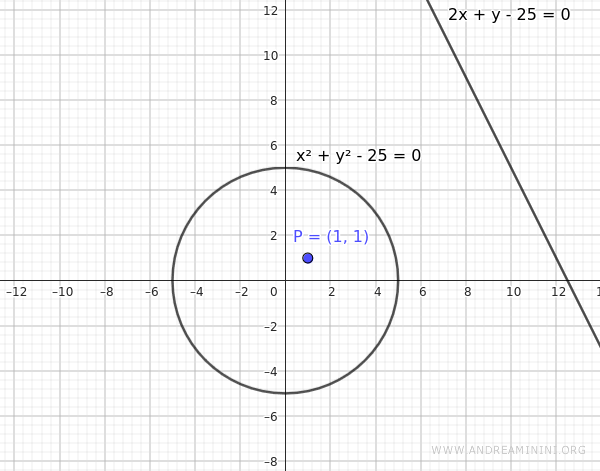
• If point P is inside the circle, there is no real tangent or secant
  If point P is inside the circle, then the equation of the line associated with the point is external to the circle. Thus, there is no real tangent or secant to the circle. However, the concept of a polar line extends to this case as well, and the polar of an internal point is still geometrically well-defined, even though it no longer represents a real tangent.

  Example: Consider the same circle from the previous example $$ x^2 + y^2 = 25 $$ but this time consider the internal point $ P(2,1) $. Apply the formula again: $$ Axx_0 + B\left(\frac{xy_0 + yx_0}{2}\right) + Cyy_0 + Dx + Ey + F = 0 $$ In this example, the coefficients are A=1, B=0, C=1, D=0, E=0, F=-25 $$ xx_0 + yy_0 - 25 = 0 $$ The coordinates of point P(2,1) are x₀=2 and y₀=1. $$ 2x + y - 25 = 0 $$ This equation represents a line external to the circle, so it is neither a real tangent nor does it intersect the circle at any point.
  

And so on.