Geometric Locus

A geometric locus is a set of points that satisfy a specific property, rule, or condition.

The defining property of a geometric locus is known as its characteristic property.

To define a geometric locus, it is necessary to demonstrate that all points in the set adhere to the same rule and that no other points satisfy this rule.

A point belongs to the geometric locus if it is one of the solutions to the locus equation_.

Purpose: The concept of a geometric locus is fundamental for defining geometric entities, curves, and surfaces through properties that can be expressed by algebraic equations.

Practical Example

From a geometric perspective, a line is a set of points that are aligned.

Thus, the characteristic property of a line is the alignment of points in a plane.

To find the points that lie on a line, you need to determine the values of x and y that satisfy the line's general equation:

$$ ax + by + c = 0 $$

In this case, the general equation of the line is the locus equation.

Example 2

The perpendicular bisector of a segment is the set of points equidistant from the segment's endpoints A and B.

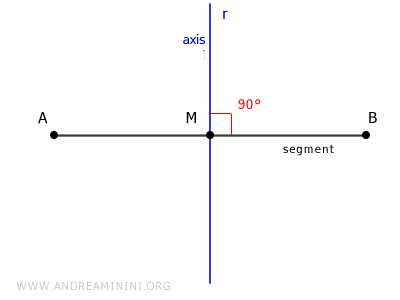
Here, the characteristic property is the equidistance from the segment's endpoints $ \overline{PA} \cong \overline{PB} $, which implies that the bisector passes through the segment's midpoint and is perpendicular (90°) to the segment.

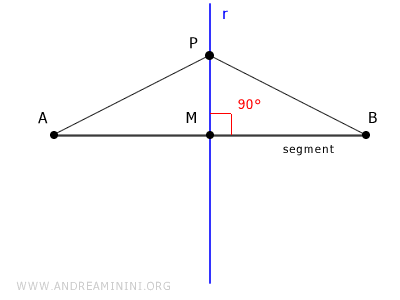
Therefore, the locus equation equates the distance of a point P(x;y) from the endpoints A(x₁;y₁) and B(x₂;y₂) of the segment:

$ \underbrace{ \sqrt{(y-y_1)^2 + (x-x_1)^2} }_{AP} = \underbrace{ \sqrt{(y-y_2)^2 + (x-x_2)^2} }_{BP} $

This equation identifies all points equidistant from the endpoints of segment AB, i.e., all points on the segment's bisector.

Explanation: In this equation, I measure the distances AP and BP using the Pythagorean theorem on triangles AMP and BMP. $$ \overline{AP} = \overline{BP} $$ $$ \underbrace{ \sqrt{ \overline{MP}^2 + \overline{AM}^2 } }_{AP} = \underbrace{ \sqrt{ \overline{MP}^2 + \overline{BM}^2 } }_{BP} $$

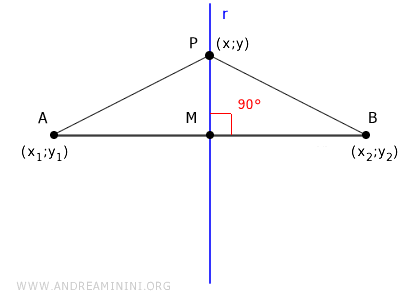
Knowing that MP=|y-y₁|=|y-y₂|, AM=|x-x₁|, and BM=|x-x₂|, I derive the equation for the equidistance of points from the segment's endpoints: $$ \underbrace{ \sqrt{(y-y_1)^2 + (x-x_1)^2} }_{AP} = \underbrace{ \sqrt{(y-y_2)^2 + (x-x_2)^2} }_{BP} $$

Other Examples of Geometric Loci

• A circle is the geometric locus of points in a plane that are at a fixed distance from a point called the "center".
• The angle bisector is the geometric locus of points equidistant from the sides of an angle.
• A parabola is the geometric locus of points in a plane that are equidistant from a fixed point (the focus) and a fixed line (the directrix).
• An ellipse is the geometric locus of points for which the sum of the distances from two fixed points (the foci) is constant.
• A hyperbola is the geometric locus of points for which the difference of the distances from two fixed points (the foci) is constant.

And so on.