Midpoint of a Line Segment

The midpoint of a line segment AB is the point that lies exactly halfway between the endpoints A and B.

For any line segment of non-zero length, there is exactly one midpoint that divides it into two equal segments.

For instance, consider the line segment AB.

 

This segment consists of an infinite number of points. However, only one point can divide it into two congruent segments—meaning two segments of equal length.

In this case, the midpoint is point C.

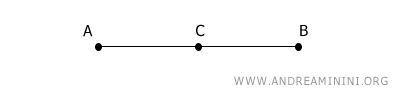
Point C divides the segment AB into two segments, AC and BC, which are congruent to each other.

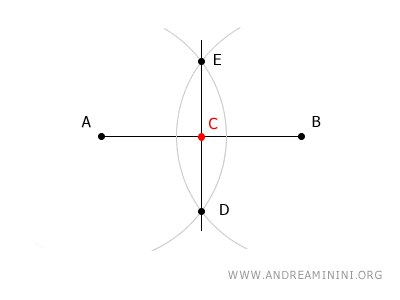
How do you find the midpoint of a segment? To find the midpoint of a segment, simply use a compass to draw two arcs centered at the endpoints of the segment. Make sure the radius is greater than half the segment's length. The intersections of the arcs will give you two points, D and E, on the line that intersects the segment AB at its midpoint C.

Given two points in the plane, $ A(x_A;y_A) $ and $ B(x_B;y_B) $, which represent the endpoints of a segment AB, the midpoint M of the segment has the following coordinates:

$$ x_M = \frac{x_A+x_B}{2} $$

$$ y_M = \frac{y_A+y_B}{2} $$

The coordinates of the midpoint M are simply the averages of the x-coordinates and y-coordinates of the endpoints.

How to Calculate the Midpoint

The coordinates M(x_M;y_M) of the midpoint M of a segment on the Cartesian plane are found by averaging the x-coordinates and y-coordinates of the endpoints A(x_A;y_A) and B(x_B;y_B).

 

The x-coordinate of the midpoint is the arithmetic mean of the x-coordinates of the segment's endpoints x_A and x_B.

$$ x_M = \frac{x_A+x_B}{2} $$

The y-coordinate of the midpoint is the arithmetic mean of the y-coordinates of the segment's endpoints y_A and y_B.

$$ y_M = \frac{y_A+y_B}{2} $$

A Practical Example

Let's consider a segment AB with endpoints A(2;3) and B(6;5).

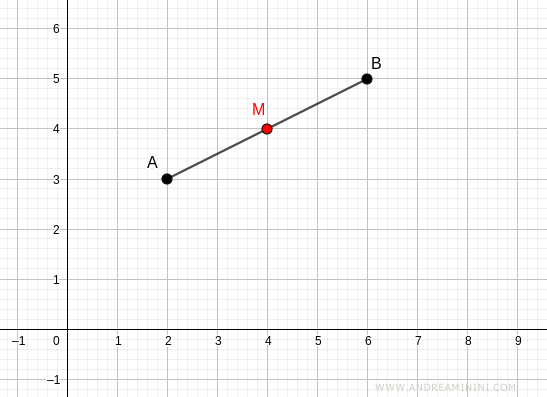
The coordinates of the midpoint are

$$ x_M = \frac{2+6}{2} = 4 $$

$$ y_M = \frac{3+5}{2} = 4 $$

The midpoint M of segment AB is located at (4;4).

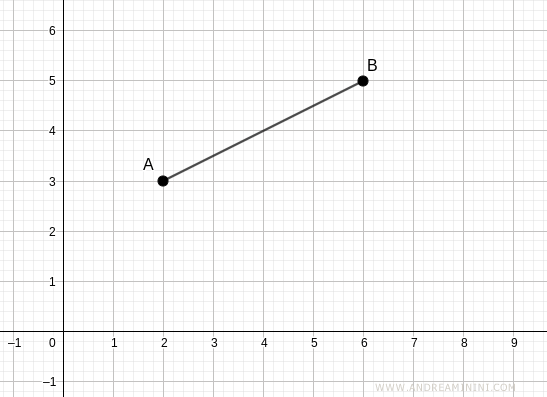
Example 2

Consider a segment AB with endpoints at A(2;1) and B(6;3).

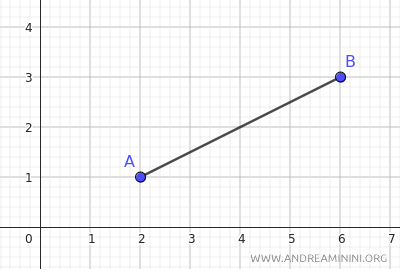
Point A is located at (2;1), so x_A=2 and y_A=1, while point B is at (6;3), so x_B=6 and y_B=3.

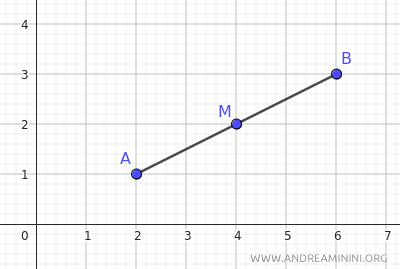
Let's calculate the coordinates of the midpoint M of segment AB:

$$ x_M = \frac{x_A+x_B}{2} = \frac{2+6}{2} = \frac{8}{2} = 4 $$

$$ y_M = \frac{y_A+y_B}{2} = \frac{1+3}{2} = \frac{4}{2} = 2 $$

The midpoint of the segment is at (x_M;y_M) = (4;2).

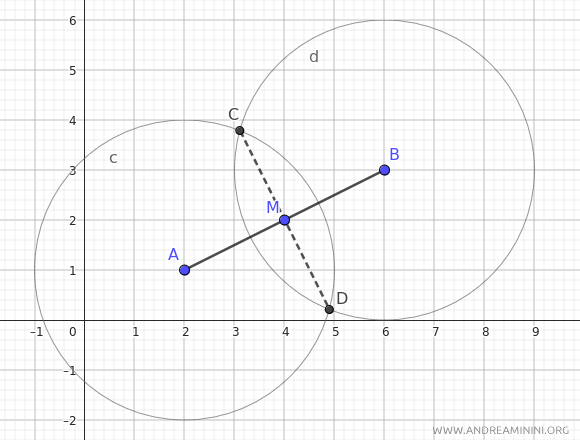
To verify, draw two arcs or circles with the same radius, as long as the radius is greater than the length of AM, centered at points A and B. Then draw a line connecting the points of intersection C and D of the arcs. The line CD will intersect segment AB at its midpoint M.

 

The Proof

Let’s consider the segment AB and its midpoint M.

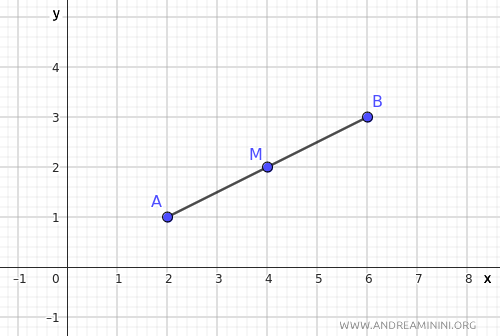
Now, draw lines parallel to the y-axis passing through points A, M, and B.

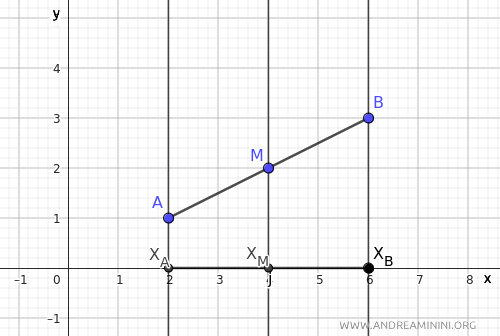
These three parallel lines are intersected by two transversals, AB and x_Ax_B.

According to the theorem of improper bundles of parallel lines, congruent segments on one transversal correspond to congruent segments on the other transversal.

Since M is the midpoint of AB, segments AM and BM are congruent. This implies that the corresponding segments x_Ax_M and x_Mx_B are also congruent.

In other words, if point M bisects segment AB, it also bisects segment X_AX_B.

$$ | x_M - x_A | = | x_B - x_M | $$

Since x_A<x_M<x_B, we can drop the absolute value.

$$ x_M - x_A = x_B - x_M $$

Solving for x_M, we get:

$$ x_M + x_M = x_B + x_A $$

$$ 2x_M = x_B + x_A $$

$$ x_M = \frac{ x_B + x_A }{2} $$

This gives us the x-coordinate of the midpoint of segment AB.

Next, we repeat the same process to calculate the y-coordinate of midpoint M.

Draw three lines parallel to the x-axis passing through points A, B, and M.

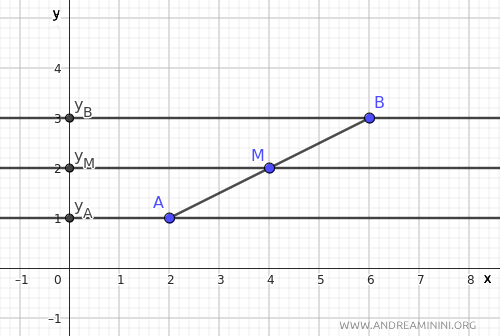
Again, these three parallel lines are intersected by two transversals, AB and y_Ay_B.

According to the theorem of improper bundles of parallel lines, if segments AM and BM are congruent, then the corresponding segments y_Ay_M and y_My_B are also congruent.

In other words, if M bisects segment AB, it also bisects its projection y_Ay_B on the y-axis.

$$ | y_M - y_A | = | y_B - y_M | $$

Since y_A<y_M<y_B, we can drop the absolute value.

$$ y_M - y_A = y_B - y_M $$

Solving for y_M, we get:

$$ y_M + y_M = y_B + y_A $$

$$ 2y_M = y_B + y_A $$

$$ y_M = \frac{ y_B + y_A }{2} $$

This gives us the y-coordinate of the midpoint of segment AB.

In summary, the coordinates of the midpoint M of segment AB are:

$$ x_M = \frac{ x_B + x_A }{2} $$

$$ y_M = \frac{ y_B + y_A }{2} $$

And so on.