Segment Bisector
The bisector of a segment is the line perpendicular to the segment that passes through its midpoint.
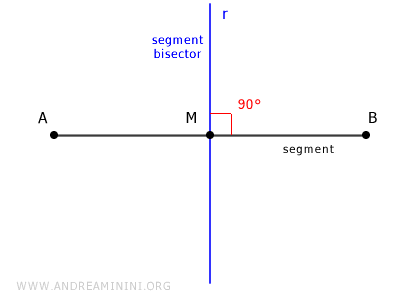
The bisector of a segment is a geometric locus because all points on the bisector are equidistant from the segment's endpoints.
For example, consider segment AB:

Point M is the midpoint of segment AB because it divides the segment into two congruent segments, AM and MB.
The bisector of segment AB is the line r that intersects the segment at its midpoint M and is perpendicular to the segment, forming a 90° angle.
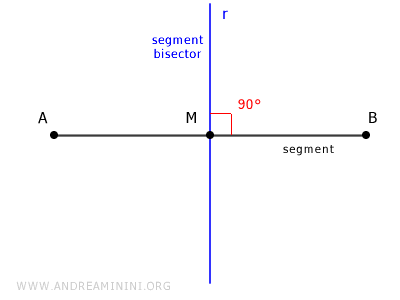
How to Find the Equation of a Segment Bisector
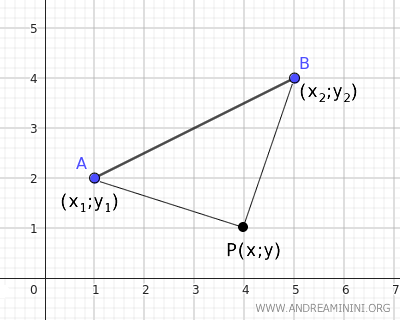
To find the equation of the bisector of segment AB, we need to find the points in the plane P(x;y) that are equidistant from the endpoints A(x1;y1) and B(x2;y2) of segment AB.
$ \underbrace{ \sqrt{(y-y_1)^2 + (x-x_1)^2 } }_{AP} = \underbrace{ \sqrt{(y-y_2)^2 + (x-x_2)^2} }_{BP} $
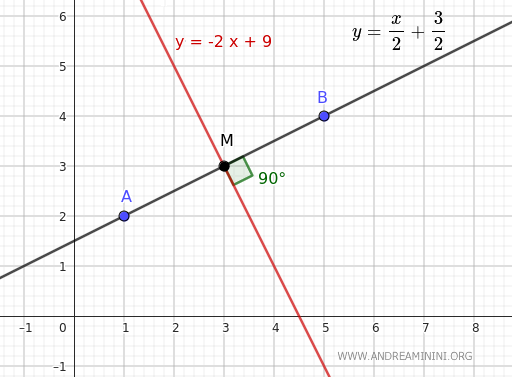
Example
Consider a segment with endpoints A(1;2) and B(5;4).
To find the equation of the bisector, we need to find the points in the plane P(x;y) that are equidistant from the endpoints A(1;2) and B(5;4) of segment AB.
$$ \underbrace{ \sqrt{(y-y_1)^2 + (x-x_1)^2 } }_{AP} = \underbrace{ \sqrt{(y-y_2)^2 + (x-x_2)^2} }_{BP} $$
Substitute the coordinates of endpoint A(1;2) into the equation: x1=1 and y1=2.
$$ \sqrt{(y-2)^2 + (x-1)^2 } = \sqrt{(y-y_2)^2 + (x-x_2)^2} $$
Then, substitute the coordinates of endpoint B(5;4) into the equation: x2=5 and y2=4.
$$ \sqrt{(y-2)^2 + (x-1)^2 } = \sqrt{(y-4)^2 + (x-5)^2} $$
Since both sides of the equation are positive, we can square both sides to simplify.
$$ ( \sqrt{(y-2)^2 + (x-1)^2 } )^2 = ( \sqrt{(y-4)^2 + (x-5)^2} )^2 $$
$$ (y-2)^2 + (x-1)^2 = (y-4)^2 + (x-5)^2 $$
Expand the binomials.
$$ y^2 -4y+4 + x^2-2x+1 = y^2-8y+16 + x^2-10x+25 $$
Eliminate the x2 and y2 terms from both sides of the equation.
$$ \require{cancel} \cancel{y^2} -4y+4 + \cancel{x^2}-2x+1 = \cancel{y^2}-8y+16 + \cancel{x^2}-10x+25 $$
Rearrange and simplify the terms.
$$ -2x -4y+5 = -10x-8y+41 $$
$$ -2x -4y+5 + 10x + 8y -41 = 0 $$
$$ 8x +4y-36 = 0 $$
Divide both sides of the equation by four to simplify the coefficients.
$$ \frac{8x +4y-36}{4} = \frac{0}{2} $$
$$ 2x +y-9 = 0 $$
Thus, we have found the equation of the line that identifies all points in the plane equidistant from the endpoints A and B of segment AB, which is the equation of the bisector of segment AB.
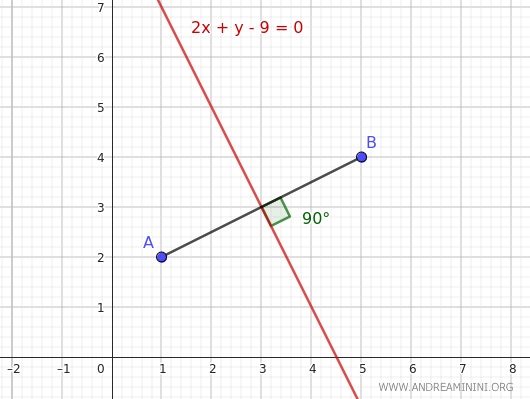
The line we found passes through the midpoint of segment AB and forms a right angle.
Proof
Consider a segment AB with endpoints A(x1;y1) and B(x2;y2). We need to find the equation of the bisector of the segment.
The bisector of the segment is a geometric locus consisting of the points in the plane P(x;y) that are equidistant from the endpoints A and B of segment AB.
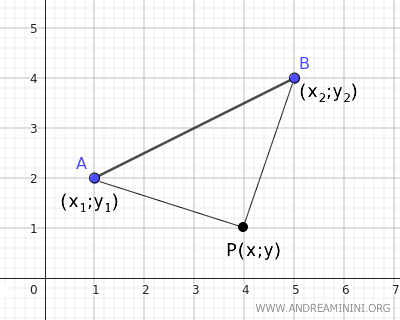
To find these points, we measure the distance of a generic point P(x;y) in the plane from the endpoints A(x1;y1) and B(x2;y2) of segment AB.
- The distance from point P to endpoint A of the segment
Segment PA measures the distance from P to point A, which can be calculated using the Pythagorean theorem in triangle ACP.
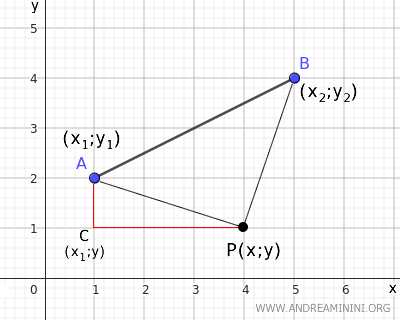
Where segment PA is the hypotenuse of right triangle ACP. Knowing that CP=|x-x1| and AC=|y-y1| $$ \overline{AP} = \sqrt{ \overline{AC}^2 + \overline{CP}^2} = \sqrt{(y-y_1)^2 + (x-x_1)^2} $$ - The distance from point P to endpoint B of the segment
Segment PB measures the distance from P to point B, which can be calculated using the Pythagorean theorem in triangle BDP.
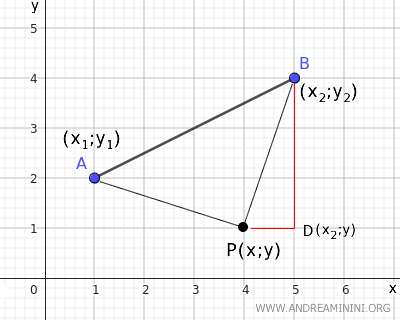
Where segment PB is the hypotenuse of right triangle BDP. Knowing that DP=|x-x2| and BD=|y-y2| $$ \overline{BP} = \sqrt{ \overline{AD}^2 + \overline{DP}^2} = \sqrt{(y-y_2)^2 + (x-x_2)^2} $$
Once we find the distance from point P to the endpoints A and B of the segment, which is the length of segments AP and BP, we set them equal to each other.
$$ \overline{AP} = \overline{BP} $$
$$ \underbrace{ \sqrt{(y-y_1)^2 + (x-x_1)^2 } }_{AP} = \underbrace{ \sqrt{(y-y_2)^2 + (x-x_2)^2} }_{BP} $$
This equation allows us to derive the equation of the bisector of the segment, knowing the coordinates of the endpoints A(x1;y1) and B(x2;y2) of segment AB.
An Alternative Method to Find the Equation of a Segment Bisector
To find the bisector of a segment, we can consider it as the line that passes through the midpoint of the segment at a right angle, forming a 90° angle.
Example
Consider the same segment as the previous example with endpoints A(1;2) and B(5;4).
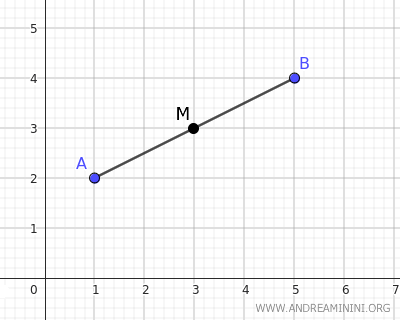
First, we find the midpoint of the segment by averaging the x and y coordinates of the two endpoints A(1;2) and B(5;4).
$$ x_M = \frac{x_A+x_B}{2} = \frac{1+5}{2} = \frac{6}{2} = 3 $$
$$ y_M = \frac{y_A+y_B}{2} = \frac{2+4}{2} = \frac{6}{2} = 3 $$
Thus, the midpoint of segment AB is at coordinates (xM;yM)=(3;3)
Now, let's derive the equation of the line containing segment AB.
The equation of the line passing through two points in the plane A(x1;y1) and B(x2;y2) is:
$$ \frac{y-y_1}{y_2-y_1} = \frac{x-x_1}{x_2-x_1} $$
Substitute the coordinates of points A(1;2) and B(5;4) into the equation: x1=1, y1=2, and x2=5, y2=4.
$$ \frac{y-2}{4-2} = \frac{x-1}{5-1} $$
$$ \frac{y-2}{2} = \frac{x-1}{4} $$
$$ 4 \cdot (y-2) = 2 \cdot (x-1) $$
Simplify the equations by dividing both sides by two.
$$ \frac{4 \cdot (y-2)}{2} = \frac{2 \cdot (x-1)}{2} $$
$$ 2 \cdot (y-2) = x-1 $$
$$ 2y-4 = x-1 $$
Finally, solve for y to get the equation of the line containing segment AB:
$$ 2y = x - 1 + 4 $$
$$ y = \frac{x+3}{2} $$
$$ y = \frac{x}{2} + \frac{3}{2} $$
Therefore, the line passing through points A and B has the equation y = x/2 + 3/2
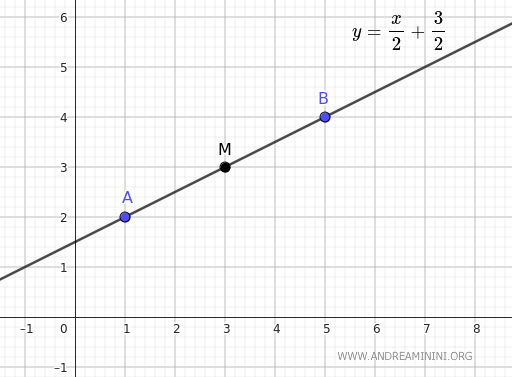
From the equation of the line y = x/2 + 3/2 in slope-intercept form, we immediately get the slope m of the line, which is m = 1/2
$$ m = \frac{1}{2} $$
Now we need to find the equation of a perpendicular line, i.e., one that forms a 90° angle.
$$ y' = m'x + c' $$
According to the perpendicularity condition, the product of the slopes m and m' of two perpendicular lines is always -1
$$ m \cdot m' = -1 $$
Substitute the slope m = 1/2 of the line containing segment AB.
$$ \frac{1}{2} \cdot m' = -1 $$
We get the slope m' = -2 of the perpendicular line.
$$ m' = -2 $$
Therefore, the equation of the perpendicular line has a slope of m' = -2.
$$ y' = m'x + c' $$
$$ y' = -2x + c' $$
To find the y-intercept c', substitute the coordinates of the midpoint M(3;3) of segment AB: x' = 3 and y' = 3
$$ 3 = -2 \cdot 3 + c' $$
$$ 3 = -6 + c' $$
$$ c' = 9 $$
After finding the y-intercept c' = 9, substitute it into the equation of the perpendicular line.
$$ y' = -2x + c' $$
$$ y' = -2x + 9 $$
Thus, we have found the line perpendicular to segment AB that passes through the midpoint M, which is the equation of the bisector of segment AB.
Observations
Some observations and notes:
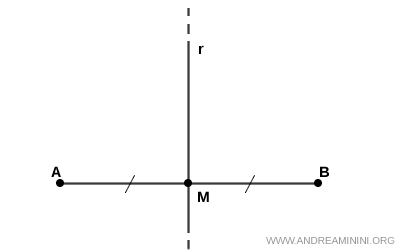
- Points symmetric with respect to an axis
Given two points A and B that define a segment AB, if a line r is the perpendicular bisector of that segment, then A and B are symmetric with respect to line r.
- Points on the bisector are equidistant from the segment's endpoints
The bisector is a geometric locus because all its points are equidistant from the endpoints A and B of the segment.Proof: Consider a point P on the bisector r of segment AB. We need to show that P is equidistant from the endpoints A and B of the segment. Knowing that r is the bisector of segment AB, we deduce that the intersection point M is the midpoint of AB, making segments AM and BM congruent (AM ≅ BM). Therefore, by the first congruence criterion (SAS), the right triangles AMP and BMP are congruent, as they have a common side (MP), a congruent side (AM ≅ AB), and the included angle congruent (90°). Being congruent, the two triangles have all congruent sides. Hence, segments AP ≅ BP are also congruent.
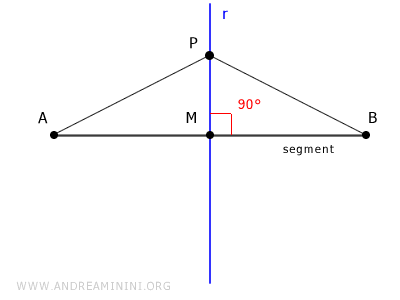
Reverse Proof: The reverse can be proven. If a point P is equidistant from the endpoints A and B, it is necessarily a point on the bisector P ∈ r. In this case, the initial hypothesis is the equidistance of point P, i.e., AM ≅ BM, and the fact that line r is the bisector of segment AB. We need to show that the equidistant point P belongs to line r. To do this, simply observe that triangle ABP is an isosceles triangle because it has two congruent sides (AM ≅ BM). As an isosceles triangle, the height corresponds to the median. Therefore, point P certainly belongs to the bisector r, which is the line perpendicular to segment AB passing through its midpoint M.
And so on.
