Commensurable and Incommensurable Segments

Two segments are commensurable if their ratio is a rational number \( \frac{a}{b} \); otherwise, they are incommensurable.

If two segments are commensurable, they can be divided into an exact number of equal parts using a shared segment as the unit of measurement.

Commensurable Segments

Two segments are described as commensurable if there exists a common unit of measurement (a reference segment) such that the lengths of both segments can be expressed as integer multiples of that unit.

Put simply, this means the ratio of their lengths is a rational number \( \frac{a}{b} \), where \( a \) and \( b \) are integers.

Example

Consider two segments with lengths of \(3\) cm and \(4\) cm.

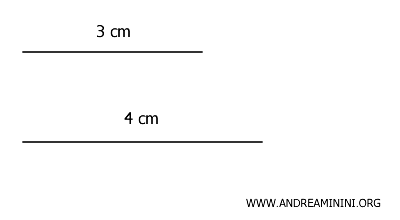
Since their ratio is \(3/4\), which is a rational number, the segments are commensurable.

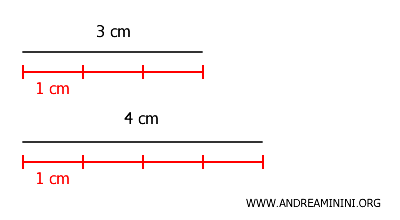
This means we can divide both segments into an exact number of equal parts using a common segment as the unit.

To identify the common segment, we calculate the greatest common divisor (GCD) of the two lengths.

$$ GCD(3, 4) = 1 $$

In this case, the greatest common divisor is 1, which means the two segments—3 cm and 4 cm—can be divided into units of 1 cm.

By breaking both segments into 1 cm units, their lengths can be expressed as \(3\) and \(4\) units, respectively.

Incommensurable Segments

Two segments are incommensurable if no common unit of measurement can express their lengths as integer multiples.

This occurs when the ratio of their lengths is an irrational number, meaning it cannot be represented as a fraction.

Example

A classic geometric example is the side and diagonal of a square.

If the side of the square is \(1\) cm, according to the Pythagorean theorem, the diagonal measures \( \sqrt{2} \) cm.

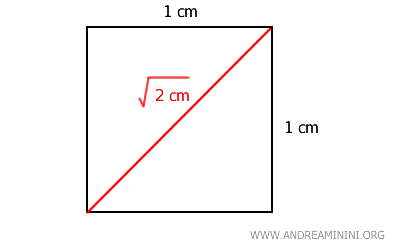
The ratio between the square’s side (\(1\)) and its diagonal (\( \sqrt{2} \)) cannot be expressed as a rational number \( \frac{a}{b} \), where \( a \) and \( b \) are integers, because \( \sqrt{2} \) is irrational.

Therefore, the two segments are incommensurable.

Note: This example posed a major challenge to the Pythagorean school, as it contradicted their belief that all ratios could be expressed as rational numbers. This discovery marked a significant turning point in the history of mathematics, leading to the concept of irrational numbers. According to tradition, the Pythagoreans sought to keep the discovery of irrationality secret, fearing it would disrupt their worldview, which was rooted in the harmony and rationality of numbers. Legend has it that the disciple who revealed this truth, Hippasus of Metapontum, was severely punished by the Pythagoreans; some accounts even suggest he was condemned to death or cast into the sea.

And so on.