Sum of Segments

Given any two segments AB and CD, the sum of their lengths is a new segment AD, which has a length equal to the combined lengths of AB and CD. $$ AB+CD = EF $$

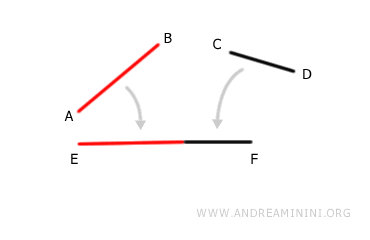
The sum of two segments follows these properties:

• Commutative Property
  For any two segments AB and CD, the sums AB+CD and CD+AB are congruent, meaning they have the same length. $$ AB+CD \cong CD+AB $$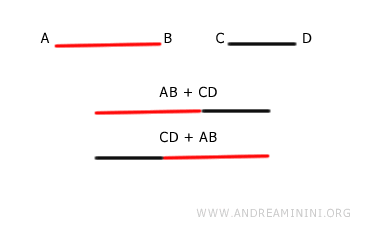

  

• Associative Property
  For any three segments AB, CD, and EF, the sums (AB+CD)+EF and AB+(CD+EF) are congruent, meaning they have the same length. $$ (AB+CD)+EF \cong AB+(CD+EF) $$
• Identity Element
  The zero segment acts as the identity element in segment addition. Adding any segment AB to the zero segment AA results in the segment AB. $$ AB + AA = AA+AB = AB $$
• Sums of Congruent Segments
  If segments AB and CD are congruent $$ AB \cong CD $$ and segments EF and GH are congruent $$ EF \cong GH $$ then their sums are also congruent. $$ AB+EF \cong CD+GH $$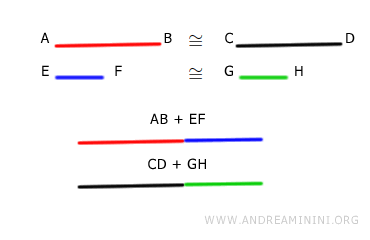

  

• Sums of Non-Congruent Segments
  If we consider two non-congruent segments $$ AB > CD $$ and two other non-congruent segments $$ EF > GH $$, the sums of these segments will also be non-congruent in the same order. $$ AB+EF > CD + GH $$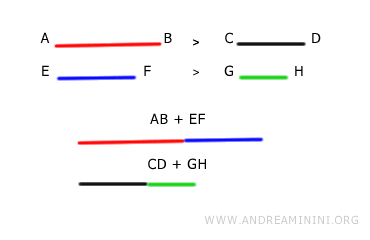

  

And so on.