Segment Transport Axiom

The Segment Transport Axiom, also known as the Segment Transport Postulate, is a fundamental geometric principle which states:

Given a ray starting from point O and a segment AB, there is a unique point P such that the segments AB and OP are congruent to each other $$ AB≌OP $$

Essentially, it is always possible to move a segment along a ray or a line without changing its shape.

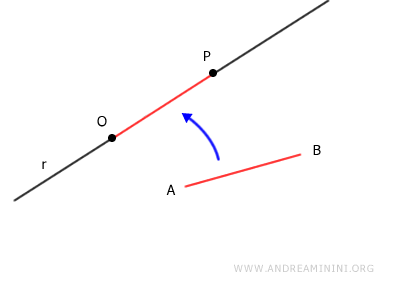
In other words, if you take a segment AB and shift it along a line r, the translated segment retains the same length and direction as the original segment.

The Segment Transport Axiom is one of Euclid's five axioms of Euclidean geometry.

Note: The other axioms include the straight-line axiom, the determined segment axiom, the angles axiom, and the parallel axiom.

This axiom underpins many theorems and proofs in Euclidean geometry.

The Proof

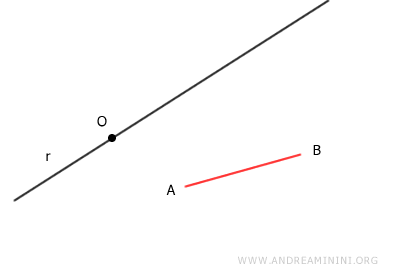
Consider any line and a segment AB.

Fix a point O on the line as the origin.

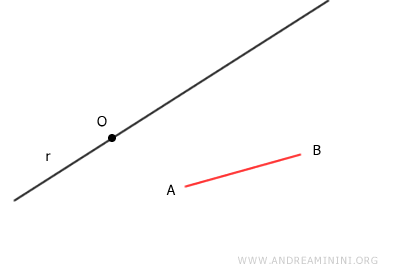
Using a compass, draw an arc with radius AB, centered at point A.

With the same compass width, draw an arc with radius AB on the line, centered at point O.

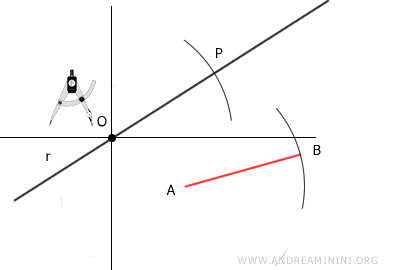
This identifies a point P on the line.

The segment OP is congruent to segment AB because it has the same length, meaning it belongs to the same congruence class.

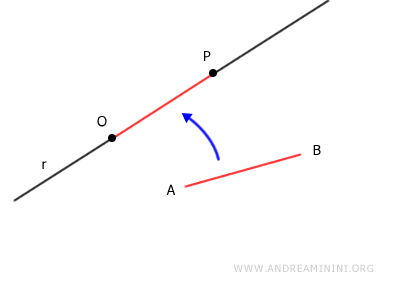
Thus, it is demonstrated that once a point O is fixed on the line, there exists one and only one segment OP that is congruent to segment AB.

And so forth.