Line Segments

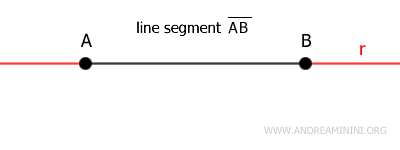
A segment is a portion of a line bounded by two points, A and B, known as endpoints.

The endpoints A and B mark the boundaries of the segment and are included within it.

Thus, the segment is depicted as a straight line starting at one point and extending to the other.

All the points between the endpoints are referred to as internal points of the segment.

Note. Despite being a bounded line, a segment consists of infinitely many points because, given any two distinct points on the segment, there is always an intermediate point between them. In other words, a segment is a dense set. The only exception is the null segment. When the endpoints coincide, the segment is called a null segment. In this specific case, the segment consists of only one point.

A segment can be considered part of a line.

The rays that belong to the same line "r" as the segment and originate from one endpoint, without passing through the other, are known as extensions of the segment.

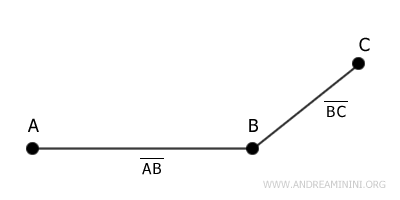
Two segments are called consecutive segments if they share an endpoint.

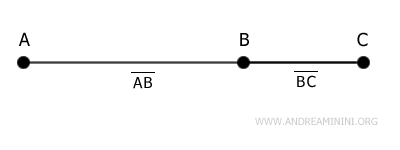
Two segments are called adjacent segments if they are consecutive and lie on the same line.

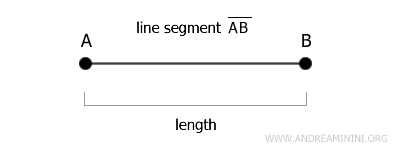
Each segment has a specific length, which is the distance between its endpoints and can be measured in units such as centimeters, meters, or other units of length.

Note. Segments are used in geometry to construct more complex shapes. They are also crucial in vector calculus as they represent the length of the vector connecting two points.

Segments that have the same length are congruent segments and, irrespective of their position in space, belong to the same class.

Note. In geometry, "congruence" means that two objects have the same shape and size but occupy different positions in space. For segments, congruence means they have the same length.

Hence, length is an equivalence class that groups multiple segments.

This differs from the measurement of length, which is simply a numerical value. For instance, a segment may be 3 cm long.

And so forth.