Subtracting Segments

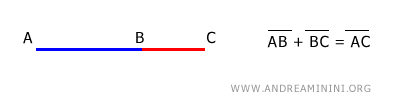
The difference between two segments AC and AB results in a segment BC such that, when BC is added to AB, the total length equals AC. $$ AC - AB = BC \Longleftrightarrow AB + BC = AC $$

For example, if segment AC is 7 units long and segment AB is 5 units long:

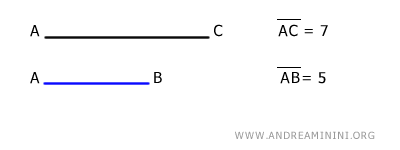
the lengths of segments AC and AB

The "subtraction" of segment AB from segment AC is the difference in their lengths:

$$ AC - AB = 7 - 5 = 2 $$

Therefore, the resulting segment BC = AC - AB is 2 units long.

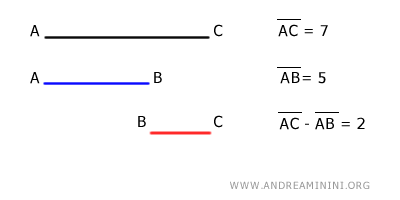
the difference AC-AB is the segment BC with a length of 2

Indeed, adding AB and BC gives us the length of AC:

$$ AB + BC \cong AC $$

Note. Starting from the sum AB+BC: $$ AB + BC $$ Knowing that BC is the difference between AC and AB, meaning BC=AC-AB: $$ AB + BC \cong AB + (AC - AB ) $$ The final result is the length of segment AC: $$ AB + BC \cong AB + (AC - AB ) \cong AC $$

Thus, the sum AB+BC is congruent to AC.

the sum AB+BC is congruent to AC

Note. In geometry, when we talk about subtracting segments, we refer to the subtraction of their lengths rather than the segments themselves. Geometry deals with lengths, angles, areas, and volumes, rather than pure numbers. Therefore, any mathematical operation (e.g., addition, subtraction, multiplication, etc.) on geometric objects relates to their measurements (e.g., lengths, areas, volumes, angles, etc.) and not to the geometric objects themselves.

Observations

Some observations about the difference between segments:

If the difference in the lengths of two segments AC and AB is zero, then segments AC and AB are congruent, meaning they have the same length. $$ AC - AB = 0 \ \ \Longrightarrow \ \ AC \cong AB $$
Example

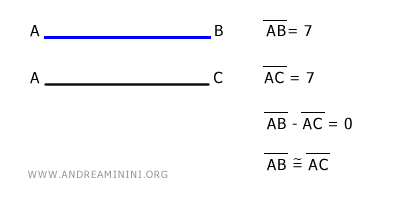
Conversely, if the difference between AB and AC is not zero, the two segments are not congruent, meaning they have different lengths. In this case, one is longer and the other is shorter.
If the difference AC-AB is positive, then the length of segment AC is greater than that of segment AB. $$ AC - AB > 0 \ \ \Longrightarrow \ \ AC > AB $$
Example
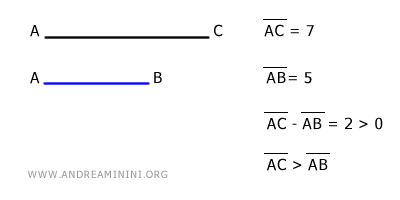
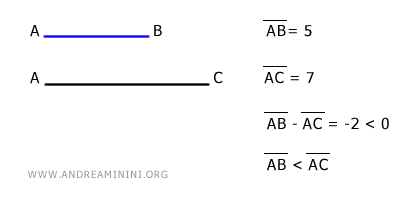
If the difference AB-AC is negative, then the length of segment AB is less than that of segment AC. $$ AB - AC < 0 \ \ \Longrightarrow \ \ AB < AC $$
Example
If AB ≅ CD and EF ≅ GH (with AB > EF), then AB - EF ≅ CD - GH, meaning the differences between two pairs of congruent segments are also congruent. $$ AB \cong CD \ , \ EF \cong GH \ | \ AB > EF \ \Longrightarrow AB - EF \cong CD - GH $$
Example

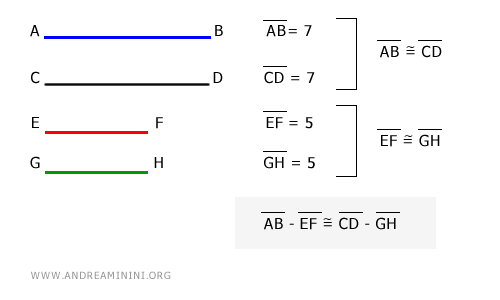
And so on.