Multiples and Submultiples of Segments

In geometry, the concepts of multiples and submultiples of a segment are similar to those used in mathematics for numbers.

  • Multiple of a Segment
    A multiple of a segment is a segment whose length is equal to the original segment's length multiplied by a natural number (N>1).

    Example. Suppose I have a segment "a" that is 6 units long and a segment "b" that is 2 units long. In this case, segment "a" is a multiple of segment "b" because it is equivalent to segment "b" multiplied by N=3, or the sum of N=3 segments each equal in length to segment "b".
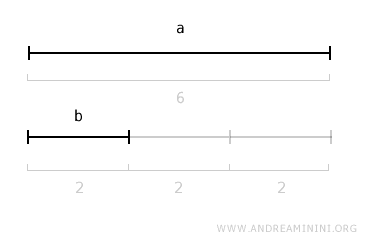
    segment "a" is a multiple of "b"

  • Submultiple of a Segment
    A submultiple of a segment is a segment whose length is equal to the original segment's length divided by a certain number (N>1).

    Example. Suppose I have a segment "a" that is 6 units long and a segment "b" that is 2 units long. In this case, segment "b" is a submultiple of segment "a" because it is equivalent to segment "a" divided by N=3.
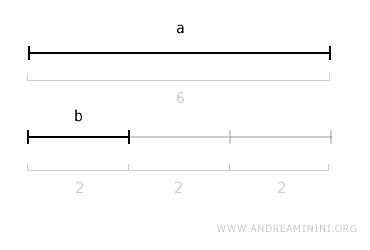
    segment "b" is a submultiple of "a"
    In practice, segment "b" is a submultiple of "a" because its length is 1/3 of segment "a" $$ a = \frac{1}{3} \cdot b $$

These concepts are very useful in geometry for expressing the relationships between the lengths of various segments in a drawing or figure.

And so on.

 

 
 
Please feel free to point out any errors or typos, or share suggestions to improve these notes. English isn't my first language, so if you notice any mistakes, let me know, and I'll be sure to fix them.

FacebookTwitterLinkedinLinkedin
knowledge base

Segments (geometry)