How to Find the Midpoint of a Line Segment

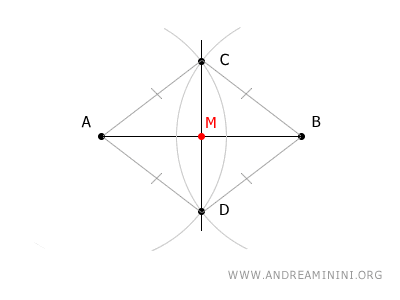
To locate the midpoint of a line segment AB, place the compass on endpoint A and open it to a width greater than half the segment's length. Draw an arc.

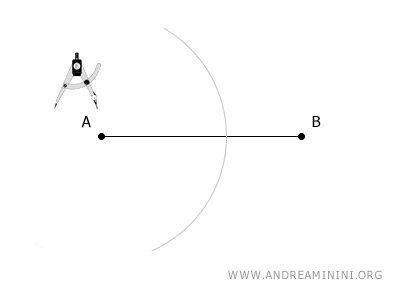
Next, position the compass on the other endpoint B and draw a second arc using the same compass width.

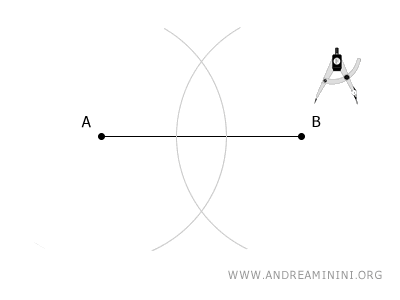
The two arcs will intersect at points C and D.

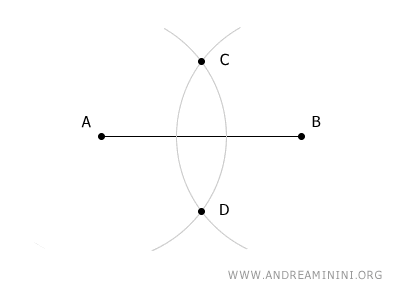
The line segment connecting points C and D intersects segment AB at its midpoint, labeled M.

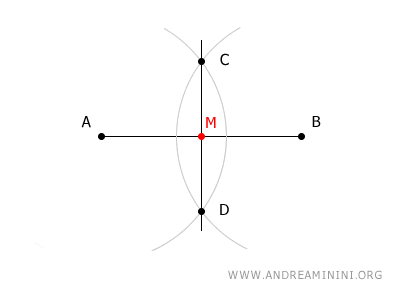
In this manner, you have found the midpoint of the segment.

Proof. By construction, the segments $ AC \cong BC \cong AD \cong BD $ are congruent. This immediately implies that triangles $ ACD $ and $ BCD $ are congruent by the third triangle congruence theorem, since they have three pairs of corresponding congruent sides.

As a consequence, corresponding angles in $ \triangle ACD $ and $ \triangle BCD $ are also congruent. In particular, the key takeaway here is that $ \angle ACD \cong \angle BCD $, which tells us that segment $ CM $ is the angle bisector of $ \angle ACB $ in $ \triangle ABC $. Since $ \triangle ABC $ is an isosceles triangle (with $ AC \cong BC $), this fact is crucial.

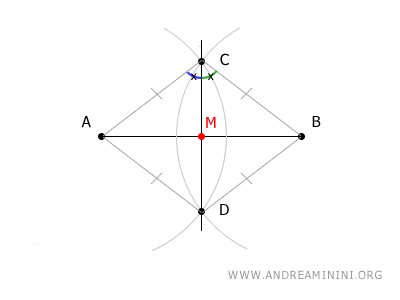
In any isosceles triangle, the angle bisector from the vertex also serves as the median. Since the median necessarily intersects the midpoint of the base $ AB $, this proves that $ M $ is the midpoint of segment $ AB $.

And that's all there is to it.