How to Construct the Angle Bisector

Let’s take any given angle α and find its bisector— the ray that splits the angle into two equal parts.

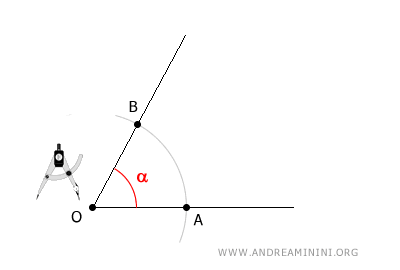
Start by placing the compass at the vertex O and drawing an arc of any radius. Make sure the arc intersects both sides of the angle.

This creates two intersection points, A and B, on the angle’s sides, both equidistant from O.

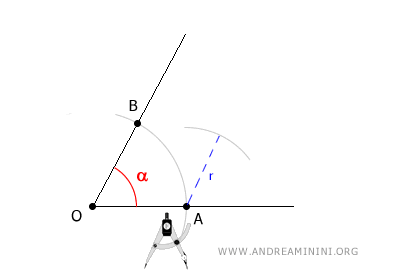
Next, place the compass at point A, set a new arbitrary radius "r" (different from the previous one if you like), and draw another arc.

Keeping the same radius "r," move the compass to point B and draw a second arc that intersects the first one.

The point where these two arcs cross is C.

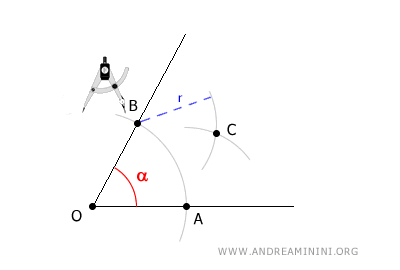
Now, draw a ray from the vertex O through point C.

The ray OC is the angle bisector—it divides α into two equal halves.

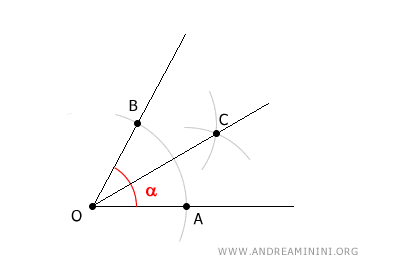
At this point, we've successfully bisected the angle α.

Proof. Let’s verify that OC is indeed the bisector. Consider the two triangles, OAC and OBC.

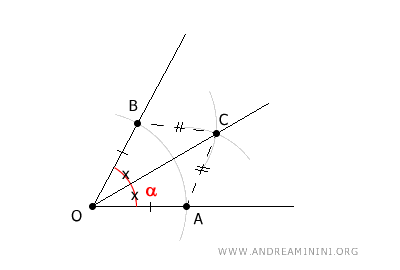
These triangles share side OC, and by construction, we know that OA = OB and AC = BC. According to the third triangle congruence criterion, this means the triangles are congruent: $$ OAC \cong OBC $$ Since corresponding angles in congruent triangles are equal, we conclude that $ A \hat{O} C \cong B \hat{O} C $, proving that OC is the angle bisector of $ A \hat{O} B $.

And that’s the proof!