How to Construct a Congruent Angle

The goal is to construct an angle congruent to angle alpha.

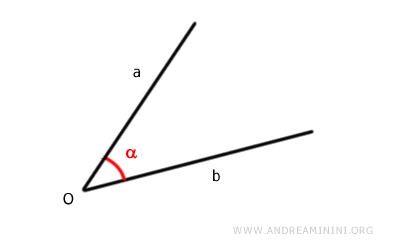
Start by placing the compass at vertex O of angle alpha. Set the compass to any convenient width and draw an arc that crosses both sides of the angle.

This creates two intersection points, A and B, on the sides of angle alpha.

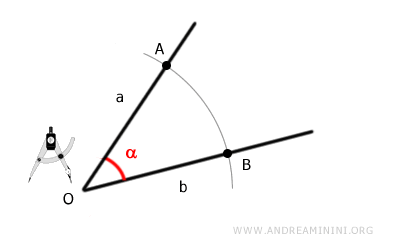
Next, draw a line segment that will serve as one side of the new, congruent angle beta.

Keeping the compass at the same width, place its point on one endpoint of the segment, which we’ll call O ("origin"), and draw an arc.

The arc intersects the segment at point C.

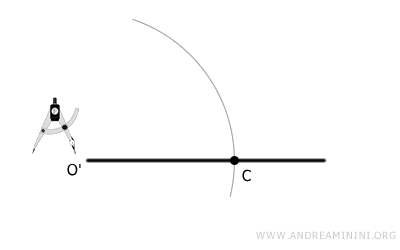
Now, adjust the compass so that its width matches the distance AB (this is the blue radius in the diagram). You can do this by placing the compass at either point A or B.

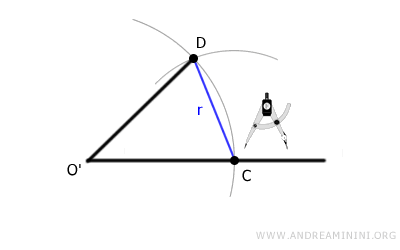
With this setting, position the compass at point C and draw a new arc. This arc should intersect the previous one at point D.

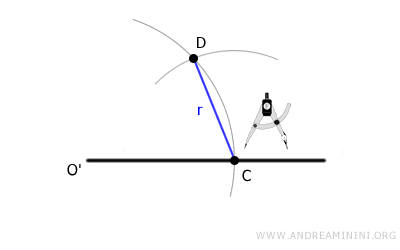
Finally, draw a second line segment connecting point O' to point D.

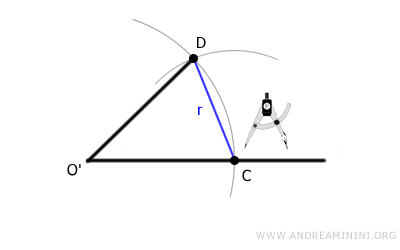
At this point, we have successfully constructed angle beta, which is congruent to angle alpha—meaning it has the same measure but is oriented differently in space.

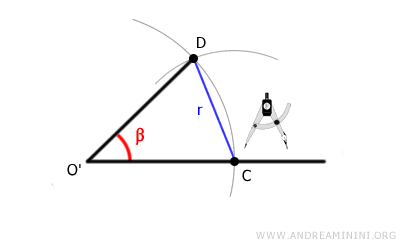
Geometric Explanation. The newly formed triangle O'CD is congruent to the original triangle OAB because their corresponding sides are congruent: OA ≅ OB ≅ O'C ≅ O'D, and AB ≅ CD. By the third triangle congruence criterion (side-angle-side), their corresponding angles must also be congruent.

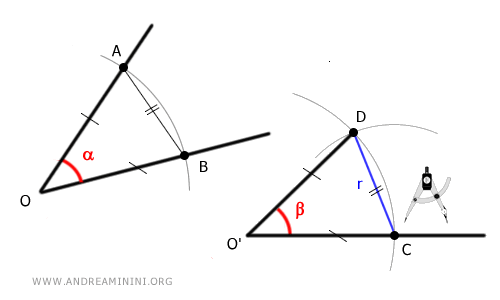
And that’s the construction!