Surfaces in Geometry

In geometry, a surface is a two-dimensional extension characterized by length and width, but lacking depth. Simply put, a surface is a region of a plane bounded by one or more closed, non-intersecting lines.

The concept of surface is an intuitive idea in elementary geometry. By "intuitive," I mean primitive, meaning it cannot be formally defined, much like a point, line, or plane.

A surface can be either closed or open.

• Closed Surface
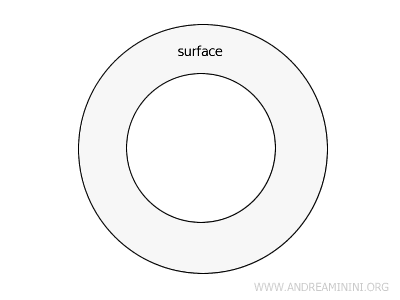
  A closed surface is confined within a finite space by a boundary (e.g., closed geometric figures, polygons, etc.). For instance, a circular ring is a closed surface bounded by two closed, non-intersecting curves. In these cases, the surface area is always calculable.
  
• Open Surface
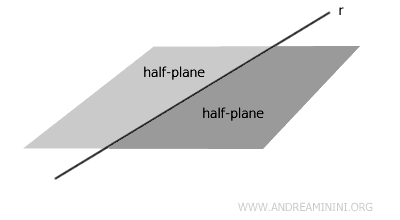
  An open surface extends infinitely in one or more directions (e.g., a plane, half-plane, or the surface between two parallel lines) in two-dimensional Euclidean space (x;y). Therefore, its area is infinite and cannot be calculated.
  

Generally, when discussing "surface" in geometry without further specification, it refers to the bounded and closed surface of a flat geometric figure.

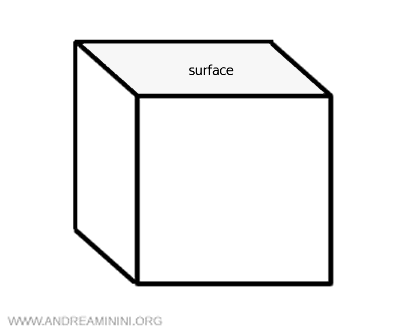
Note: A surface can also be viewed as a set of points in three-dimensional Euclidean space (x;y;z). In fact, the concept of a surface arises from the need to measure the boundary of a solid object. For example, in the case of a cube, the surface is the sum of the areas of the squares on each face.

Types of Surfaces

There are two main types of surfaces: flat surfaces and curved surfaces.

• Flat Surfaces
  A flat surface is entirely devoid of curvature, extending uniformly and consistently in all directions within a plane. It can be limited to a finite region of space or not. In a more theoretical and mathematical context, it corresponds to the concept of a plane, an abstract notion that extends infinitely.

  An example of a flat surface is a sheet of paper. However, it should be noted that a sheet of paper has a physical thickness, albeit minimal. A flat surface, on the other hand, is a more abstract concept without thickness. In simple terms, in plane geometry, the thickness of a surface can be ignored even if it exists.

• Curved Surfaces
  Unlike flat surfaces, curved surfaces exhibit variation in their shape. They are not flat. These surfaces can also be confined to a region of space or extend infinitely in all directions. Curved surfaces possess a higher level of geometric complexity compared to flat surfaces.

  Common examples of curved surfaces include the surface of a sphere or a cylinder. Both are closed surfaces that enclose Euclidean space. Curved surfaces are studied in non-Euclidean geometries.
  

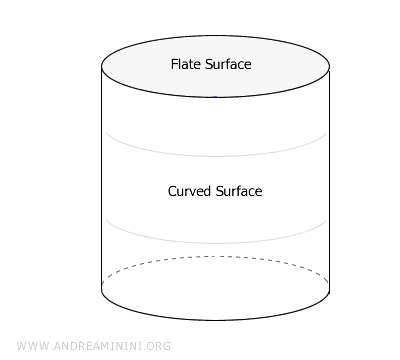
In addition to these categories, modern mathematics also considers surfaces in spaces with more than three dimensions. This concept exceeds our intuitive ability to visualize but plays a crucial role in scientific fields such as topology.

Equivalent Surfaces

Two surfaces are equivalent when they have the same extent, i.e., the same area.

For example, a triangle and a square are equivalent surfaces when they have the same area, even though their shapes are different and they are not congruent figures.

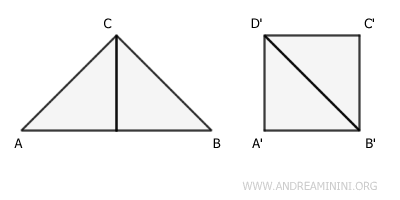
When two surfaces are equivalent, they belong to the same equivalence class.

Note: This last example also demonstrates that equivalence between two figures does not imply congruence. Congruent figures are always equivalent, but the reverse is not always true. Equivalent figures may not be congruent.

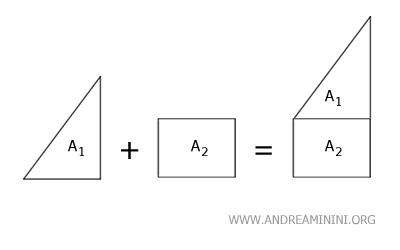
Sum and Difference of Surfaces

The sum of two non-overlapping surfaces S₁ and S₂ is equal to the sum of their respective areas Area(S₁)+Area(S₂).

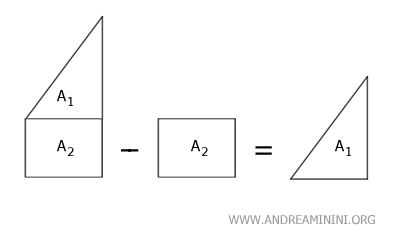
Similarly, the difference between two non-overlapping surfaces S₁ and S₂ is equal to the difference of their areas Area(S₁)-Area(S₂).

Comparing Surfaces

When comparing surfaces, the outcome can be one of the following:

• Equivalent Surfaces
  Surfaces are equivalent if they have the same extent (area).
  
• Larger Surface
  A surface is larger if it has a greater extent (area) than another. This means the figure occupies more space.
  
• Smaller Surface
  A surface is smaller if it has a lesser extent (area) than another. This implies that the figure occupies less space.
  

And so on.