Theorem of Equivalence Between a Parallelogram and a Triangle

A triangle is equivalent to a parallelogram that has the same height and half the base of the triangle.

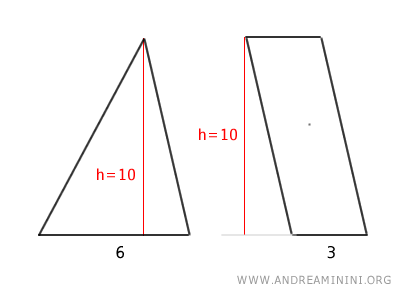
Alternatively, a triangle is equivalent to a parallelogram that has the same base and half the height of the triangle.

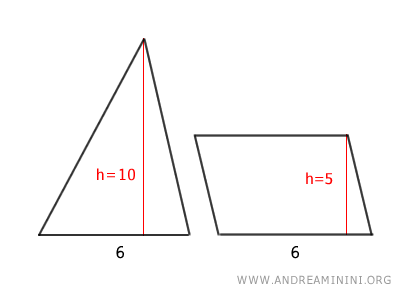
In other words, if a triangle has the same height and a base twice as long as that of the parallelogram, the areas are equal.

The same applies when the triangle has the same base and twice the height of the parallelogram.

A Practical Example

Let's consider a triangle and a parallelogram.

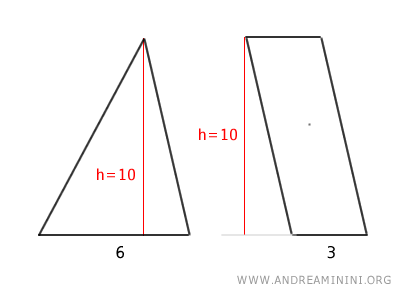
The triangle and the parallelogram have the same height h=10.

Additionally, the base of the triangle is 6, which is exactly double the base of the parallelogram (3).

Therefore, according to the equivalence theorem, they have the same area.

$$A_p = A_t$$

Where A_p and A_t are the areas of the parallelogram and the triangle, respectively.

The area of the parallelogram A_p is calculated by multiplying the base (3) by the height (10).

$$A_p = 3 \cdot 10 = 30$$

Thus, the area of the triangle A_t is also 30.

$$A_t = 30$$

Example 2

In this case, the parallelogram has the same base as the triangle (b=6) and half the height (h_p=5) of the triangle (h_t=10).

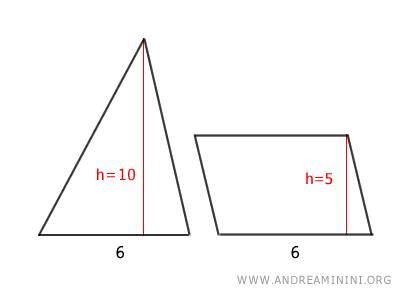
According to the equivalence theorem, the two polygons are equivalent because they have the same area.

$$A_p = A_t$$

Where A_p and A_t are the areas of the parallelogram and the triangle.

The area of the parallelogram A_p is the product of the base (6) and the height (5).

$$A_p = 6 \cdot 5 = 30$$

Therefore, the area of the triangle A_t is also 30.

$$A_t = 30$$

Proof

A] Parallelogram with the Same Height and Half the Base of the Triangle

To prove the theorem, consider a triangle ABC and a parallelogram DEFG.

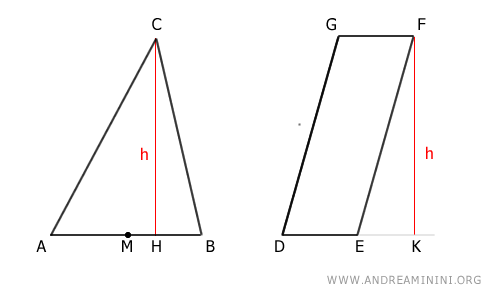
Where M is the midpoint of segment AB.

$$\overline{AM} \cong \overline{BM}$$

Initially, the heights of the two geometric figures are congruent.

$$\overline{CH} \cong \overline{FK}$$

The corresponding base of the parallelogram's height is congruent to half the base of the triangle.

In other words, the base of the triangle (AB) is twice the base of the parallelogram (DE).

$$\overline{AB} \cong 2 \cdot \overline{DE}$$

or

$$\overline{AM} \cong \overline{BM} \cong \overline{DE}$$

We need to prove that the two figures ABC and DEFG are equivalent, meaning they have the same area.

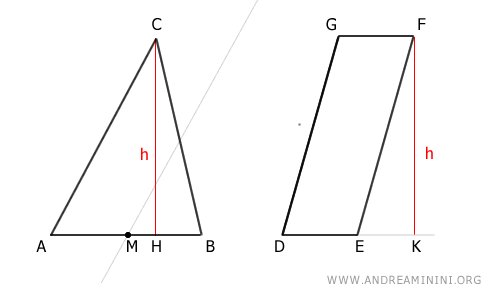
Draw a line parallel to side AC of the triangle that passes through its midpoint.

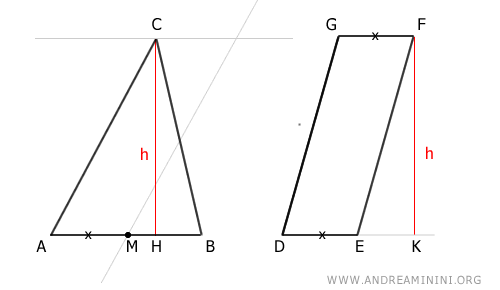
Then draw a line parallel to side AB of the triangle that passes through vertex C.

This creates another parallelogram AMNC.

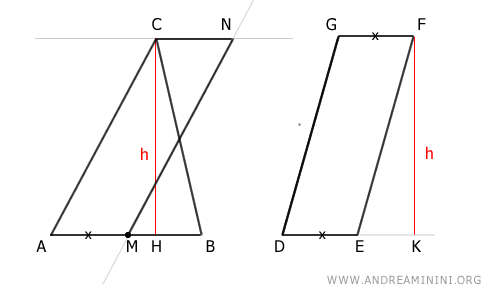
According to the theorem of equivalence of parallelograms, parallelogram AMNC is equivalent to parallelogram DEFG because it has the same base (AM ≅ DE) and height (CM ≅ FK).

$$AMNC \cong DEFG$$

Now, angles α ≅ δ and β ≅ γ are congruent because they are alternate interior angles of a transversal between two parallel lines (parallel lines theorem).

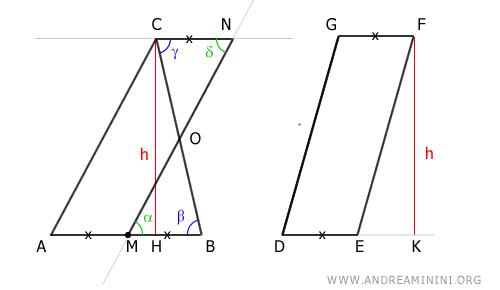
Since BM ≅ AM because M is a midpoint and the opposite sides of a parallelogram are parallel, we also deduce that sides BM ≅ CN are congruent.

Thus, triangles MBO and CNO are congruent by the second criterion of triangle congruence, as they have one congruent side BM ≅ CN and congruent adjacent angles α ≅ δ and β ≅ γ.

$$MBO \cong CNO$$

Since they are congruent, triangles MBO and CNO are also equivalent areas, meaning they have the same area.

$$MBO \doteq CNO$$

To simplify, I color the equivalent areas MBO and CNO in gray.

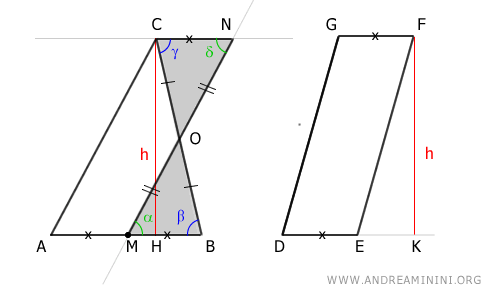
At this point, triangle ABC can be seen as the sum of trapezoid AMOC and triangle MBO.

$$ABC \doteq AMOC + MBO$$

Similarly, parallelogram AMNC can be seen as the sum of trapezoid AMOC and triangle CNO.

$$AMNC \doteq AMOC + CNO$$

Knowing that triangles MBO and CNO are equivalent, we deduce that triangle ABC and parallelogram AMNC are equivalent because they are composed of the same trapezoid AMC and equivalent triangles CNO and MBO.

$$ABC \doteq AMOC + MBO \doteq AMOC + CNO \doteq AMNC$$

$$ABC \doteq AMNC$$

 

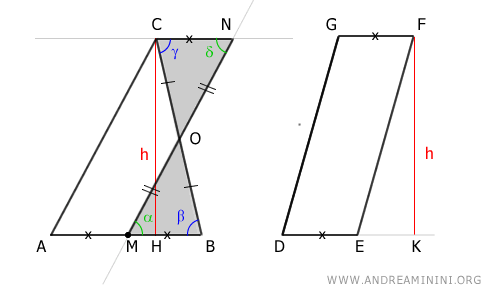
Since parallelogram AMNC is equivalent to parallelogram DEFG, we deduce that triangle ABC and parallelogram DEFG also have equivalent areas, meaning they are equivalent polygons.

$$ABC \doteq DEFG$$

This proves the first part of the theorem.

B] Parallelogram with the Same Base and Half the Height of the Triangle

To prove the second part of the theorem, which is symmetrical to the first, we will follow a different reasoning.

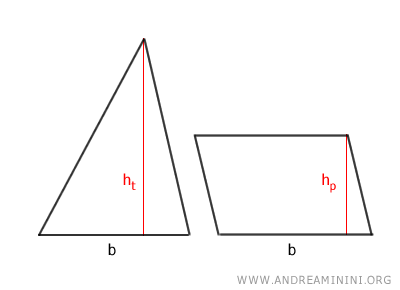
In this case, the reasoning is logical-mathematical and is based on the fact that the area of the triangle is half the product of its base (b_t) and height (h_t).

$$A_t = \frac{b_t \cdot h_t}{2}$$

While the area of the parallelogram is the product of its base (b_p) and height (h_p).

$$A_p = b_p \cdot h_p$$

Now, assuming the bases of the triangle and parallelogram are equal,

$$b_p = b_t$$

Thus, denoting the common base as b=b_t=b_p, the area formulas become:

$$A_t = \frac{b \cdot h_t}{2}$$

$$A_p = b \cdot h_p$$

The triangle and the parallelogram are equivalent when they have the same area.

$$A_t = A_p$$

$$\frac{b \cdot h_t}{2} = b \cdot h_p$$

Simplify by dividing both sides by b.

$$\frac{b \cdot h_t}{2} \cdot \frac{1}{b} = b \cdot h_p \cdot \frac{1}{b}$$

$$\frac{h_t}{2} = h_p$$

Therefore, the triangle and the parallelogram have the same area when the height of the parallelogram $h_p = \frac{h_t}{2}$ is half the height of the triangle.

The theorem is proven.

Note: This logical reasoning can also be applied to prove the first part of the theorem, where the triangle and the parallelogram have the same height. $$A_t = \frac{b_t \cdot h_t}{2}$$ $$A_p = b_p \cdot h_p$$ In this case, the height is the same h=h_t=h_p. $$A_t = \frac{b_t \cdot h}{2}$$ $$A_p = b_p \cdot h$$ The two polygons are equivalent when they have the same area $$A_t = A_ p$$ $$\frac{b_t \cdot h}{2} =b_p \cdot h$$ Simplify the equation by dividing both sides by h. $$\require{cancel} \frac{b_t \cdot \cancel{h}}{2} =b_p \cdot \cancel{h}$$ $$\frac{b_t}{2} =b_p$$ This demonstrates that the two polygons have the same area when the base of the parallelogram (b_p) is half the base of the triangle (b_t).

And so on.