Parallelogram Equivalence Theorem
Two parallelograms are equivalent if they have congruent bases and corresponding heights.
This is one of the most well-known criteria for equivalence.
A Practical Example
Consider these two parallelograms.
Although they have different shapes, both parallelograms have the same base (b=5) and height (h=3).
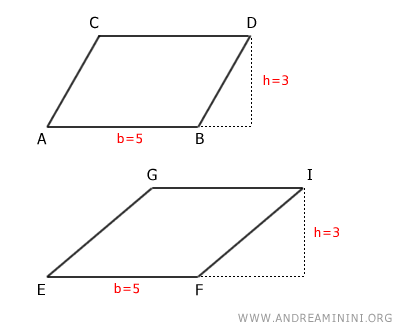
Therefore, their areas are equal.
To verify this, we just need to use the formula for the area of a parallelogram.
$$ A = b \cdot h $$
Where "b" is the base and "h" is the height of the parallelogram.
$$ A = b \cdot h = 5 \cdot 3 = 15 $$
The result is the same for both parallelograms.
The Proof
To prove this theorem, let's consider two parallelograms, ABCD and EFGI.
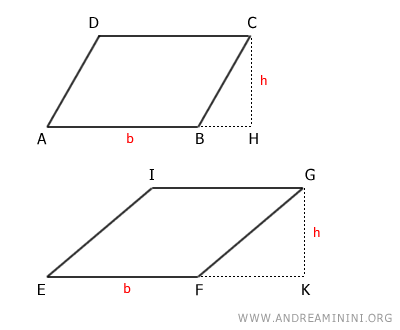
By our initial assumption, the two parallelograms have congruent bases and congruent heights.
$$ \overline{AB} \cong \overline{EF} $$
$$ \overline{HC} \cong \overline{KG} $$
We need to prove that the two parallelograms are equivalent, meaning they have the same area.
To do this, we align the bases AB and EF of the two parallelograms with a rigid motion.
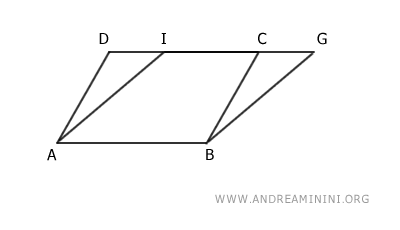
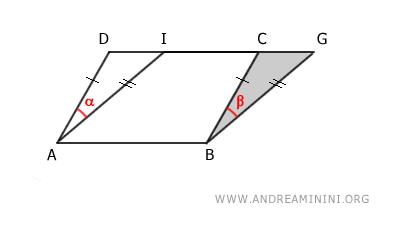
This alignment reveals two triangles, ADI and BCG.
The angles α and β of the triangles are congruent because the sides of the angles are parallel and coincide with those of the parallelograms, which are, by definition, parallel AD≅BC and AI≅BG.
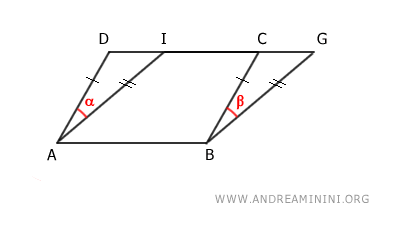
Therefore, by the first congruence criterion, the two triangles ADI≅BCG are congruent because they have two congruent sides AD≅BC and AI≅BG and the included angle α≅β.
$$ ADI \cong BCG $$
Now, the area of parallelogram ABCD can be seen as the difference between trapezoid ABGD and triangle BCG.
$$ ABCD \doteq ABGD - BCG $$
Similarly, the area of parallelogram ABGI can be considered as the difference between trapezoid ABGD and triangle ADI.
$$ ABGI \doteq ABGD - ADI $$
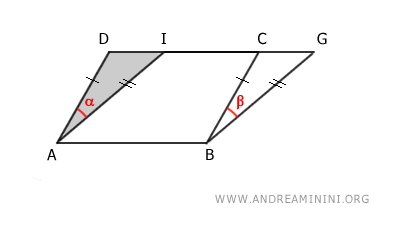
Knowing that triangles ADI≅BCG are congruent, we can deduce that the areas of parallelograms ABCD and ABGI are the same (equivalent areas) because both are obtained by the difference of two congruent polygons.
$$ ABCD \doteq ABGD - BCG \doteq ABGD - ADI \doteq ABGI $$
$$ ABCD \doteq ABGI $$
Since, by construction, parallelograms ABGI≅EFGI are congruent, we deduce that the original parallelograms ABCD and EFGI are equivalent polygons, meaning they have the same area.
$$ ABCD \doteq EFGI $$
Observations
Some remarks, corollaries, and side notes:
- Two rectangles are equivalent if they have congruent bases and heights
Rectangles are specific cases of parallelograms with right angles. Therefore, the parallelogram equivalence theorem also applies to rectangles.
And so on.
