Equivalent Surfaces

Two surfaces A and B are considered equivalent surfaces when they have the same extent. $$ A \doteq B $$

In Euclidean plane geometry, this means the surfaces are equivalent if they have the same area.

$$ Area(A) = Area(B) $$

This is the most common and intuitive form of equivalence.

For example, a square and a triangle are equivalent surfaces if their areas are equal, even though their shapes are different.

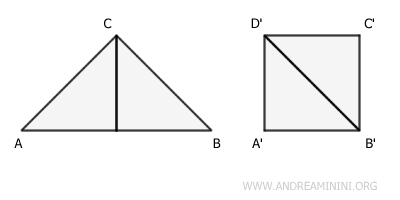
All surfaces with the same extent (area) belong to the same equivalence class.

Properties of Equivalent Surfaces

The equivalence of surfaces is an equivalence relation, which means it satisfies the following properties:

• Reflexive Property
  A surface is always equivalent to itself. $$ A \doteq A $$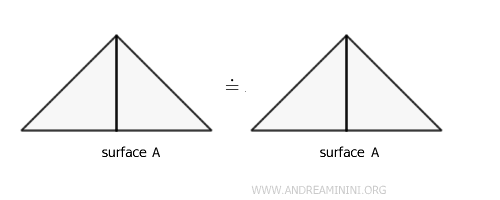

  

• Symmetric Property
  If surface A is equivalent to surface B, then surface B is also equivalent to surface A. $$ A \doteq B \Leftrightarrow B \doteq A $$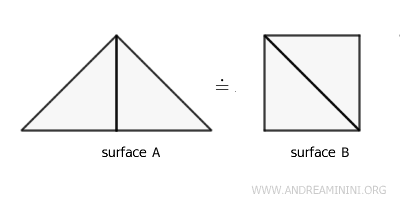

  

• Transitive Property
  If surface A is equivalent to surface B, and surface B is equivalent to surface C, then surface A is also equivalent to surface C. $$ A \doteq B \ , \ B \doteq C \Longrightarrow A \doteq C $$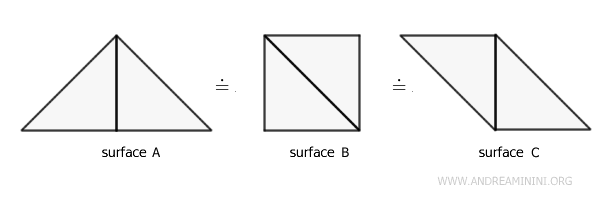

  

These are key concepts in mathematics that extend beyond simple geometry, as they apply to all equivalence relations.

Additional Observations

Here are some additional notes and observations about equivalent surfaces:

• De Zolt's Postulate
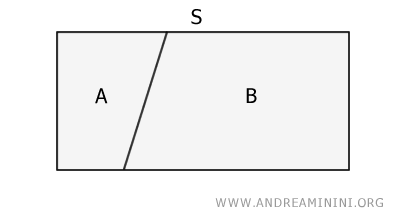
  A surface is not equivalent to a part of itself.

  Example. Surface S is divided into two parts, A and B. The area of surface S is the sum of the areas of surfaces A and B. Therefore, S cannot be equivalent to surface A or B.
  

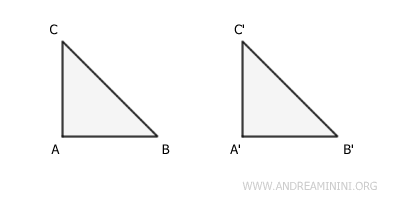
• Two congruent surfaces are always equivalent, but the reverse is not always true
  For example, two congruent triangles have the same side lengths and angle measures in the same order. Therefore, they have the same area and are equivalent surfaces.
  
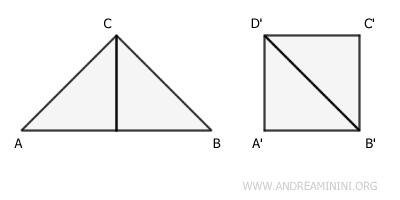
  Conversely, a triangle ABC and a square ABCD with the same area are equivalent surfaces but not congruent because they cannot be superimposed point by point with a rigid motion. They have different sides and angles.
  
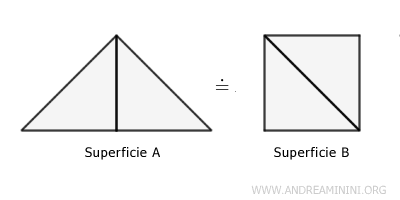
• Principle of Equidecomposability
  Two equidecomposable figures, meaning they can be divided into the same number of congruent parts, are considered equivalent.
  
• If you start with two congruent figures and then add or remove congruent parts, the resulting figures will still be equivalent.
• If we consider two pairs of equivalent surfaces $$ S_1 \doteq S_2 $$ $$ S_3 \doteq S_4 $$ and add them together, the sum of the surfaces is also equivalent $$ S_1 + S_3 \doteq S_2 + S_4 $$

  Example
  

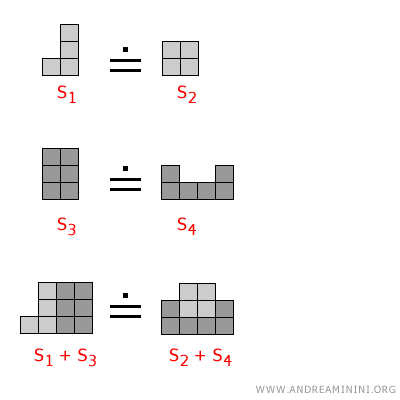
• If we consider two pairs of equivalent surfaces $$ S_1 \doteq S_2 $$ $$ S_3 \doteq S_4 $$ and subtract them, the difference of the surfaces is also equivalent $$ S_1 - S_3 \doteq S_2 - S_4 $$

  Example
  

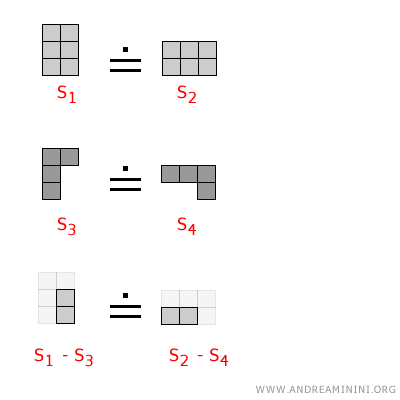
And so on.