De Zolt’s Postulate for Surfaces

What does De Zolt’s postulate state?

A surface can never be equivalent to the individual surfaces (i.e., parts) that compose it.

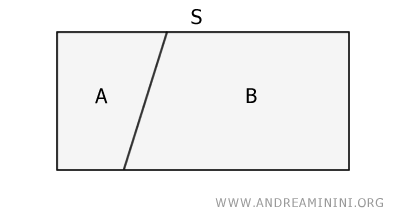
This is a fairly intuitive notion: no part of an object can be equivalent to the whole.

That’s precisely why it’s framed as a “postulate.”

What is a postulate? A postulate is a statement or principle within a mathematical or scientific framework that is accepted as true without proof. It serves as a foundational assumption from which further theorems and laws are logically derived.

Let’s take, for instance, an arbitrary surface S.

Suppose we draw a line that divides surface S into two distinct regions, which we’ll label A and B.

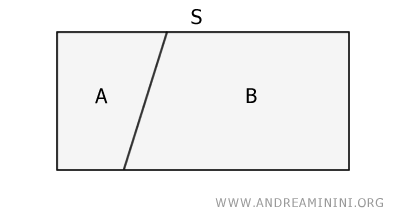
Two surfaces are considered equivalent if and only if they have the same area.

In this case, the total area of surface S is the sum of the areas of A and B:

$$ Area(S) = Area(A) + Area(B) $$

It follows, then, that neither A nor B can be equivalent to S, nor can S be equivalent to either of its parts.

In other words, a surface can never be equivalent to one of its constituent parts.

And so forth.