Equivalence Theorem of a Triangle and a Polygon Inscribed in a Circle
A triangle OHK and a polygon ABCDE (regular or irregular) inscribed in a circle are equivalent $$ ABCDE \doteq OHK $$ if the height of the triangle is equal to the radius of the circle and the base of the triangle is equal to the perimeter of the polygon.
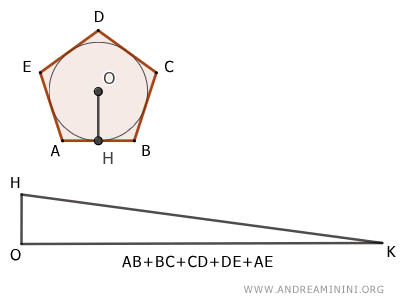
In geometric terms, this means that in a polygon circumscribed, the area can be calculated as if it were a triangle with the height equal to the radius of the circle and the base equal to the perimeter of the polygon.
$$ Area = \frac{ perimeter \ × \ radius}{2} $$
Knowing that a regular polygon is always inscribed in a circle, I deduce that all regular polygons are equivalent to a triangle.
However, only some irregular polygons can be inscribed in a circle.
In practice, this means that the area of polygons meeting these criteria can be calculated as if they were triangles with specific base and height measurements. To prove this theorem, simply divide the polygon into many triangles with heights equal to the radius of the circle.
An Example
As an example, let's consider a regular pentagon ABCD where each side is 2 units long.
The pentagon inscribes a circle with a radius OH = 1.38.
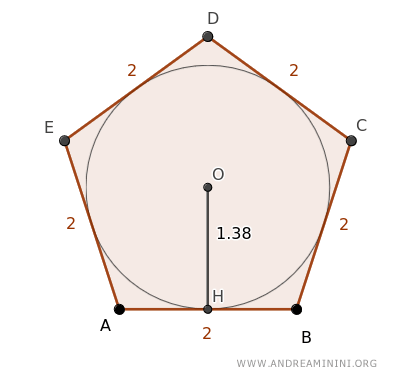
Being a polygon circumscribed, I can apply the equivalence theorem to calculate its area as if it were a triangle.
The perimeter of the pentagon is P=10
$$ P = \overline{AB} + \overline{BC} + \overline{CD} + \overline{DE} + \overline{AE} = 2+2+2+2+2 = 10 $$
So, we consider a triangle FGI with base FG=10, congruent to the perimeter of the polygon FG≅P and height IF=1.38, congruent to the radius of the circle IF≅OH.
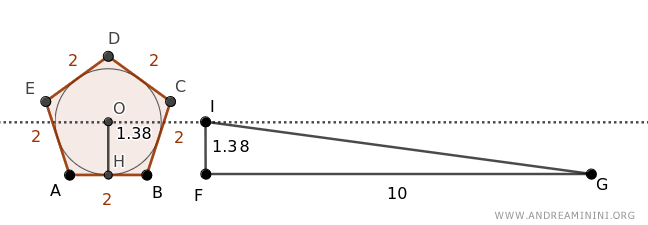
The area of the triangle is equal to half the product of the base and height.
$$ A_t = \frac{b \cdot h}{2} = \frac{10 \cdot 1.38}{2} = \frac{13.8}{2} = 6.9 $$
Therefore, the area of the equivalent triangle is 6.9
$$ A_t = 6.9 $$
Consequently, the area of the pentagon is also 6.9
$$ A_p = A_t = 6.9 $$
In this way, I obtained the area of the pentagon without calculating it directly.
To verify the result, I calculate the area of the regular pentagon using the planar geometry formula. $$ A_p = \frac{n \cdot l \cdot a}{2} $$ Where n=5 is the number of sides of the regular polygon, l=2 is the length of the sides, and a=1.38 is the apothem. $$ A_p = \frac{5 \cdot 2 \cdot 1.38}{2} = \frac{13.8}{2} = 6.9 $$ The calculation is exactly the same.
The Proof
Consider a polygon ABCDE inscribed in a circle with center O and radius OH.
The number of sides of the polygon or whether the polygon is regular or irregular does not matter, as long as it is inscribed in a circle.
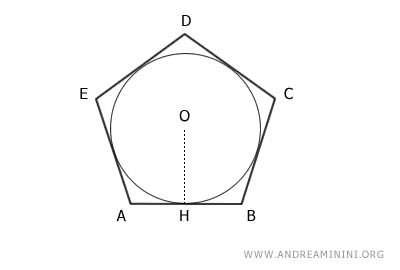
The perimeter of the polygon is the sum of its sides
$$ P = \overline{AB} + \overline{BC} + \overline{CD} + \overline{DE} + \overline{AE} $$
I connect the center of the circle O with all the vertices of the polygon.
This divides the polygon into five triangles: ABO, BCO, CDO, DEO, AEO
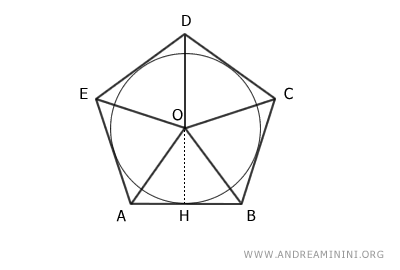
I add segments connecting the center of the circle O with the points of intersection between the circle and the polygon.
These segments, being radii, are all congruent with the segment OH.
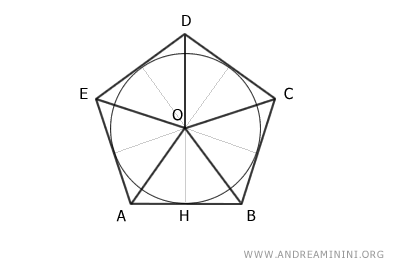
Therefore, the polygon ABCDE is equivalent to the sum of five triangles
$$ ABCDE \doteq ABO + BCO + CDO + DEO + AEO $$
Now I arrange the sides of the polygon consecutively on a single line.
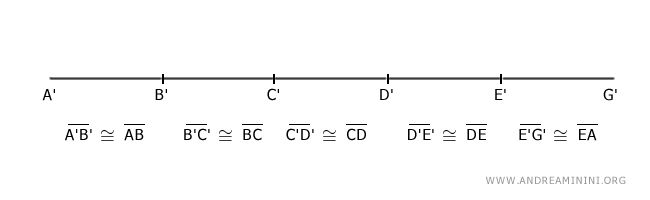
It is evident that the segment A'G' is congruent with the perimeter AB+BC+CD+DE+AE of the polygon ABCDE.
$$ \overline{A'G'} \cong \overline{AB} + \overline{BC} + \overline{CD} + \overline{DE} + \overline{AD} $$
I add to the end A' of A'G' a perpendicular segment A'F'≅OH congruent with the radius of the circle (OH).
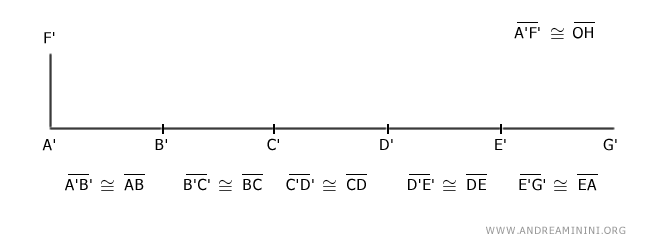
Finally, I draw segments connecting point F' with points B', C', D', E', G'.
This way, I obtain five triangles.
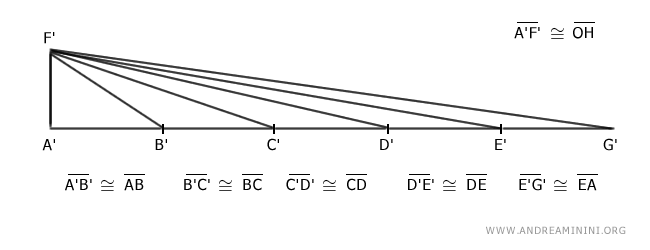
By construction, triangle A'G'F' has a base equal to the perimeter of the polygon AB+BC+CD+DE+EA and height A'F' equal to the radius of the circle inscribed in the polygon.
Moreover, triangle A'G'F' is equivalent to the sum of five smaller triangles.
$$ A'G'F' \doteq A'B'F' + B'C'F' + C'D'F' + D'E'F' + E'G'F' $$
According to the principle of triangle equivalence, triangles A'B'F' and ABO are equivalent because they have the same height OH≅A'F' and the same base AB≅A'B'.
$$ A'B'F' \doteq ABO $$
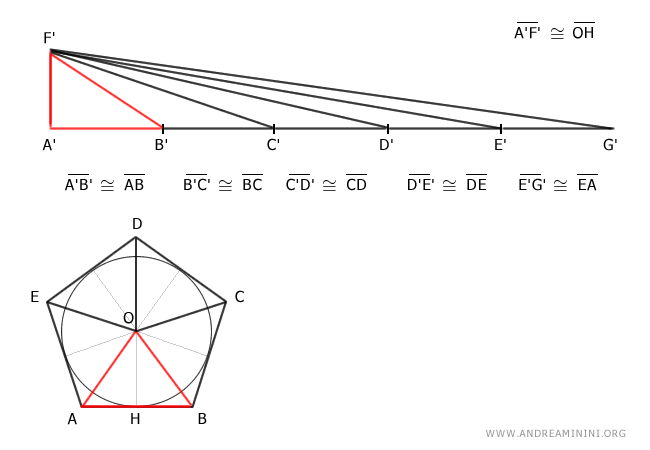
For the same reason, the other triangles are also equivalent
$$ B'C'F' \doteq BCO $$
$$ C'D'F' \doteq CDO $$
$$ D'E'F' \doteq DEO $$
$$ E'G'F' \doteq AEO $$
We already know that triangle A'G'F' is equivalent to the sum of the areas of five triangles.
$$ A'G'F' \doteq A'B'F' + B'C'F' + C'D'F' + D'E'F' + E'G'F' $$
We also know that the triangles making up A'G'F' are equivalent to the triangles making up the polygon ABCDE. Thus, the two polygons are equicomposed polygons.
$$ A'G'F' \doteq ABO + BCO + CDO + DEO + AEO $$
$$ A'G'F' \doteq ABO + BCO + CDO + DEO + AEO \doteq ABCD $$
Therefore, I deduce that polygon ABCDE is equivalent to triangle A'G'F' which has the base as the perimeter of the polygon and the height as the radius of the circle inscribed in the polygon.
$$ A'G'F' \doteq ABCD $$
This demonstrates that they have the same area, meaning they are equivalent.
And so on.
