Polygons Circumscribed about a Circle

A polygon is considered circumscribed about a circle when all its sides touch the circle at tangent points.

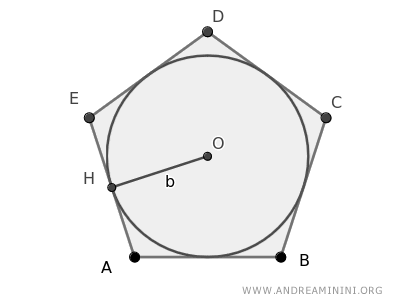
This configuration also means that the circle is inscribed within the polygon.

The center of this inscribed circle is known as the incenter, and its radius is referred to as the inradius.

The circle itself is called the incircle.

Not every polygon can be circumscribed about a circle. For instance, all triangles can be circumscribed. However, only those quadrilaterals where the sums of the lengths of opposite sides are equal can be circumscribed. By definition, all regular polygons, such as pentagons and hexagons, are circumscribed about a circle because being regular implies that each side equally touches a common circle.

Area of Circumscribed Polygons

The area of a regular polygon circumscribed about a circle is calculated as the semiperimeter (p) multiplied by the radius (r) of the circle $$ A = p \cdot r $$

This formula is based on the principle that a circumscribed polygon can be equated to a triangle whose base equals the polygon's perimeter (P) and whose height is the radius (r) of the circle.

Given that the area of a triangle is half the product of its base and height, this leads to the area formula for the circumscribed polygon.

$$ A = \frac{P \cdot r}{2} = \frac{P}{2} \cdot r = p \cdot r $$

Here, P represents the perimeter, and p the semiperimeter, so P equals 2p.

As the radius (r) of the circle aligns with the apothem (a) of the regular polygon, the area of a regular polygon can also be found by multiplying the semiperimeter by the apothem (a).

$$ A = p \cdot a $$

Example

Take for instance this regular pentagon circumscribed about a circle with a known area of A=15.48.

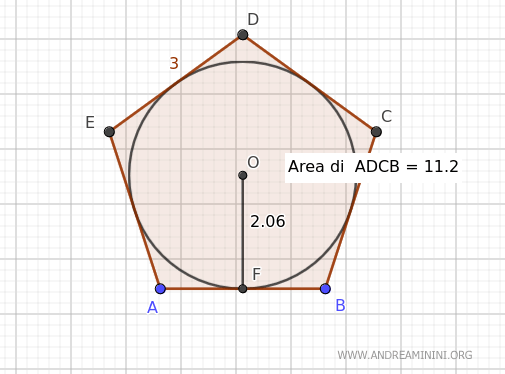
The length of one side is 3, and the radius of the inscribed circle is 2.06.

The semiperimeter of the pentagon is 7.5.

$$ p = \frac{3 \cdot 5}{2} = \frac{15}{2} = 7.5 $$

Multiplying it by the circle's radius yields the pentagon's area exactly.

$$ A = p \cdot r = 7.5 \cdot 2.06 = 15.48 $$

Dividing the pentagon into five triangles for demonstration, the area of each triangle is calculated as the base (the side of the pentagon) times the height (the radius of the circle) divided by two.

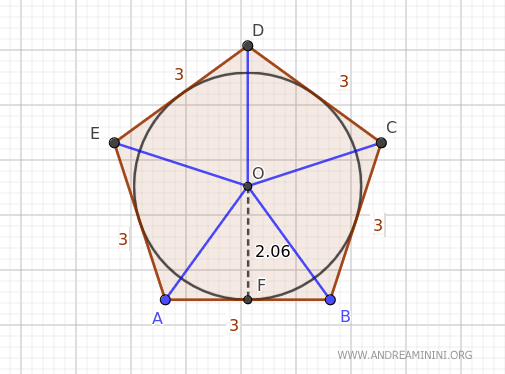
The sum of these triangles' areas gives us the total area of the pentagon.

$$ A = 5 \cdot \frac{3 \cdot 2.06}{2} = \frac{5 \cdot 3}{2} \cdot 2.06 $$

Where the semiperimeter (5·3)/2 and the radius 2.06 yield the same result, the area of the regular pentagon.

$$ A \cong 15.48 $$

This method is applicable to any regular polygon, as they can all be circumscribed about a circle.

Circumscribed Polygon Theorem

A convex polygon can only be circumscribed about a circle if all angle bisectors intersect at a common point (the incenter).

If the bisectors do not converge at a common point, the polygon cannot be circumscribed about a circle.

The converse also holds true: if a convex polygon is circumscribed about a circle, then the angle bisectors will meet at a singular point, the incenter of the inscribed circle.

Triangles and regular polygons inherently have an incenter where their bisectors meet. Only certain irregular polygons, those circumscribed about a circle, share this characteristic.

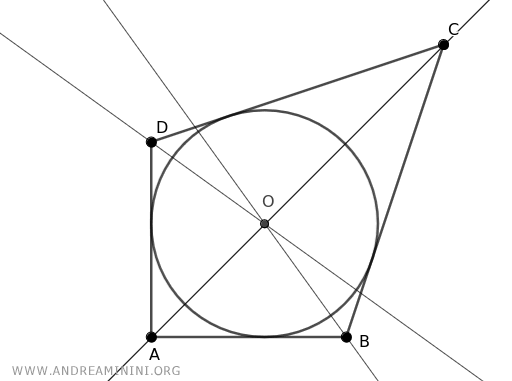
A Practical Example

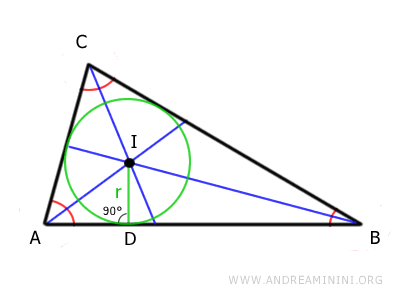
For example, the bisectors of a triangle's angles always converge at a point known as the incenter.

Drawing a circle centered at this incenter (I) with a suitable radius (r) makes the circle tangent to all the triangle's sides.

Demonstrating the Theorem

To demonstrate the theorem, consider a polygon whose angle bisectors meet at a common point O.

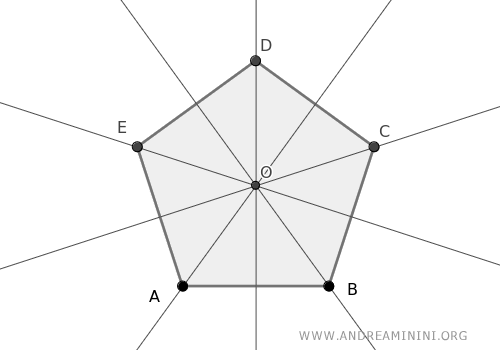
An angle's bisector is defined as the line dividing the angle into two equal parts.

The challenge is to prove the polygon can be circumscribed about a circle.

By definition, the bisector represents points equidistant from the polygon's sides.

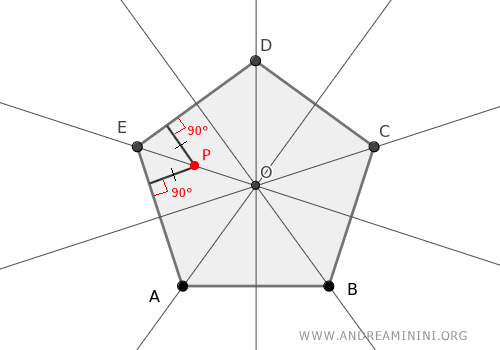
Thus, the intersection point O is equally distant from all polygon sides.

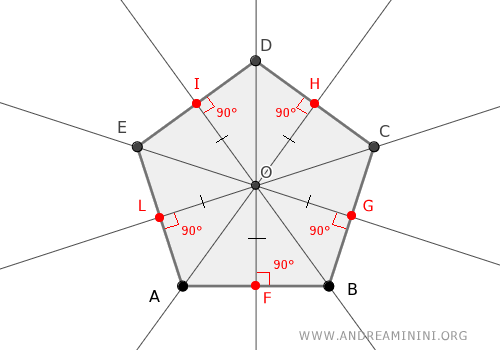
Meaning, a circle (the incircle) with radius equal to this distance d that touches all the polygon sides can be drawn at point O.

This circle, tangent to the polygon's sides, confirms that the polygon is circumscribed about a circle.

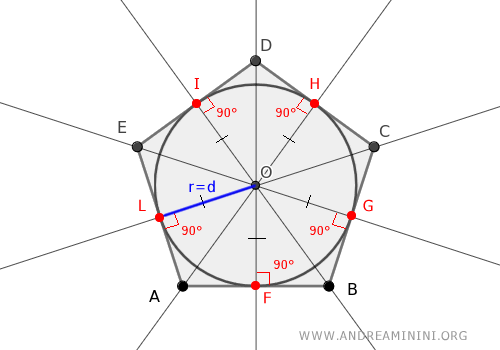
Thus, the theorem is proven.