The Secant Similarity Theorem in a Circle

Drawing two secants from an external point P to a circle creates a situation where the segments on one secant act as the extremes, and those on the other as the means of a proportion, and vice versa.

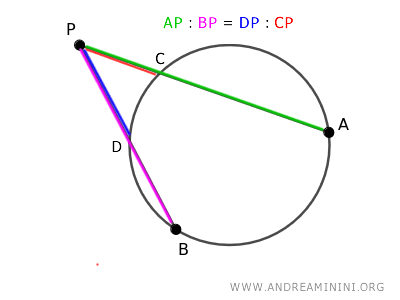
A Practical Example

In this example, I have a circle and two secants originating from the same external point P.

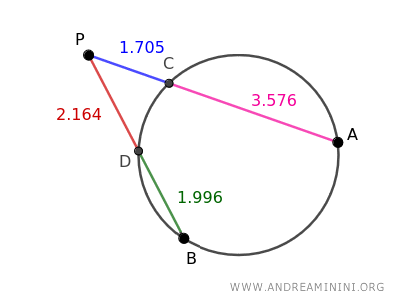
The segment AP measures 5.281

$$ \overline{AP} = \overline{AC} + \overline{CP} = 1.705 + 3.576 = 5.281 $$

The segment BP measures 4.16

$$ \overline{BP} =  \overline{BD} + \overline{DP} = 2.164 + 1.996 = 4.16 $$

Checking if the theorem's proportion holds true

$$ \overline{AP} : \overline{BP} = \overline{DP} : \overline{CP}  $$

Substituting the segment values

$$ 5.281 : 4.16 = 2.164 : 1.705  $$

$$ 1.269 = 1.269  $$

The theorem holds, with the segments of one secant as the extremes of the proportion and those of the other as the means.

Note. I've rounded the two quotients to three decimal places (1.269) because the segment measurements AP, BP, CP, and DP from Geogebra are rounded values.

The Proof

Consider a circle and an external point P.

Draw two distinct secant lines AP and BP.

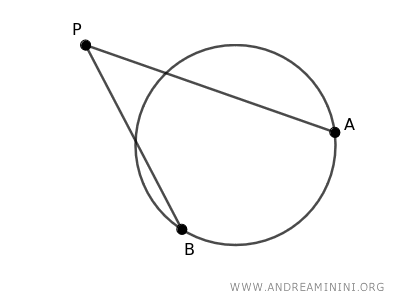
The intersection points C and D of the secants with the circle divide the secants into two segments: AC+CP and BD+DP

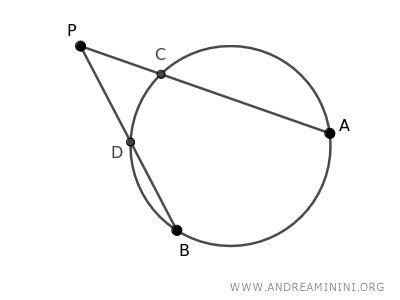
Draw segments connecting the intersection of one secant with the extremity of the other secant, namely segments AD and BC.

This forms two triangles, ADP and BCP.

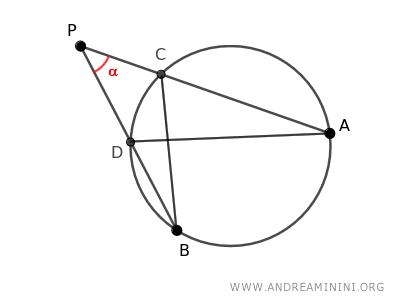
The two triangles ADP and BCP share the same angle α.

The other two angles β and γ are congruent angles β≅γ because they are both circumferential angles that intercept the same arc CD.

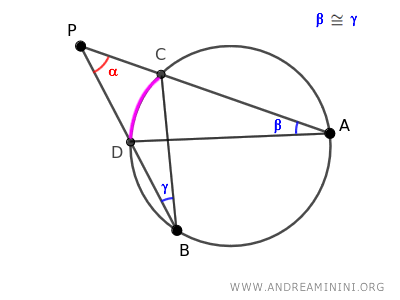
Therefore, by the first criterion of triangle similarity, the two triangles ADP and BCP are similar, having two congruent angles α and β≅γ.

$$ ADP \approx BCP $$

Being similar, their corresponding sides are proportional.

$$ \overline{AP} : \overline{BP} = \overline{DP} : \overline{CP} = \overline{AD} :  \overline{BC}   $$

This confirms the proportionality between the segments:

$$ \overline{AP} : \overline{BP} = \overline{DP} : \overline{CP}  $$

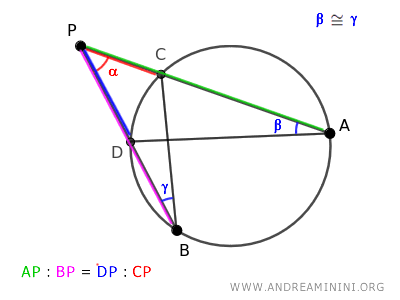
And so on.