Central Angle of a Circle

A central angle is positioned at the center of a circle, extending its sides to intersect the circumference at two points, which defines an arc.

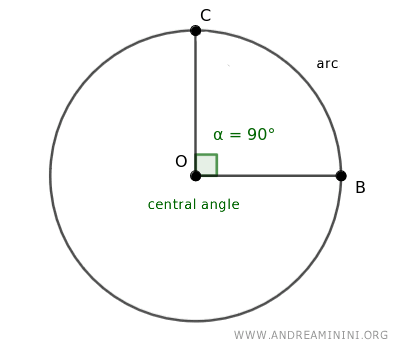
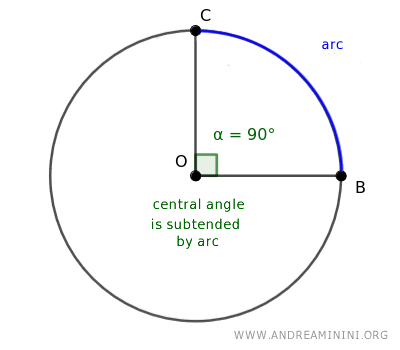
This angle is known to subtend the arc, indicating that the arc corresponds to the angle itself.

In essence, the central angle encompasses the arc, with the arc reflecting the central angle.

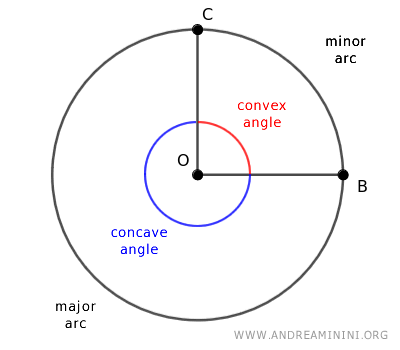
Typically, drawing two rays from the center of a circle to its circumference creates two angles: one concave (over 180°) and one convex (under 180°), or alternatively, two straight angles (180°).

l

The convex angle subtends a smaller arc, while the concave angle subtends a larger one.

Central vs. Inscribed Angles: A Distinction. These represent distinct geometric concepts. A central angle's vertex is located at the circle's center, whereas a inscribed angle is on the circle's perimeter.

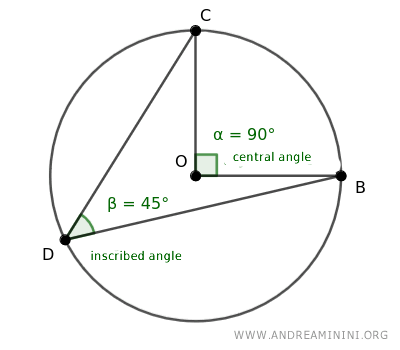
A central angle (α) and a circumferential angle (β) are considered corresponding when they span the same arc.

For any given arc AB, there exists a single central angle (α) that subtends the arc, alongside an infinite number of corresponding circumferential angles (β, β',...).

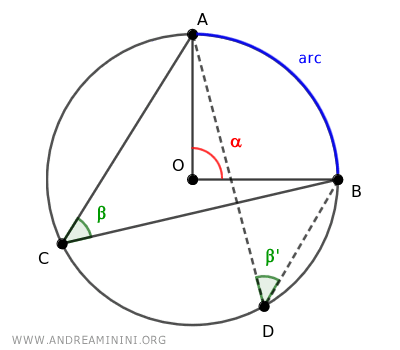
All corresponding circumferential angles that subtend the same arc are congruent (β≅β') and are half the size of their corresponding central angle (β=α/2).

Insights on Central Angles

A few key points and observations about central angles:

• Central angles are twice the size of any corresponding circumferential angles
  For instance, with a central angle α, any circumferential angle β=α/2 corresponding to it will be half the size of the central angle.
  
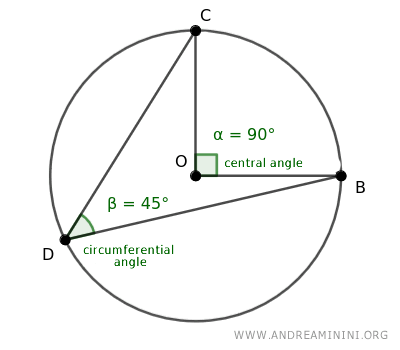
• Proportionality of the central angle to the subtended arc
  The size of the central angle is directly proportional to the size of the subtended arc, and vice versa. A central angle of 360° spans the entire circle, while a 180° angle spans a semicircle.
• Congruency of Angles
  Within a circle, two central angles are congruent (equal in size) only if the arcs they subtend are equally long. Additionally, if one arc is longer than another, the central angle subtending the longer arc will be larger than the angle subtending the shorter arc.
• Sum of Angles
  The sum of central angles subtending two separate, non-overlapping arcs equals the angle subtended by the combined arcs.
• The bisector of a central angle not only splits the angle in half but also bisects the corresponding arc and stands perpendicular to the arc’s chord.

And so forth.