Inner and Concentric Circles
A circle is inside another circle, called the outer circle, if the distance between their centers \( OO' \) is less than the difference of their radii: $$ \overline{OO'} < | r - r' | $$
Here, \( OO' \) represents the distance between the centers of the two circles, while \( r \) and \( r' \) are the radii of the outer and inner circles, respectively.
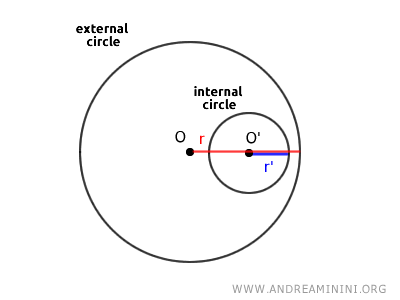
In this context, the assumption is that all points of one circle lie within another circle.
This can occur only if two conditions are satisfied:
- The center of the inner circle \( O' \) is located within the outer circle.
- The radius of the inner circle \( r' \) plus the distance between the centers \( OO' \) is less than the radius of the outer circle: $$ \overline{OO'} + r' < r $$
These conditions ensure that all points of the inner circle are contained within the outer circle.
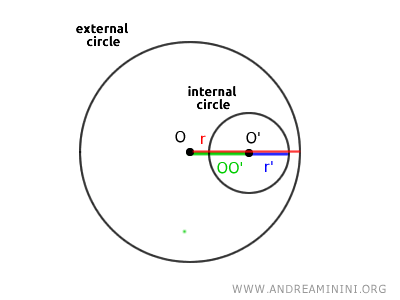
Note: In the special case where the two circles share the same center \( O = O' \) but have different radii \( r \ne r' \), they are called concentric circles. In this scenario, the distance between the centers is zero \( OO' = 0 \).
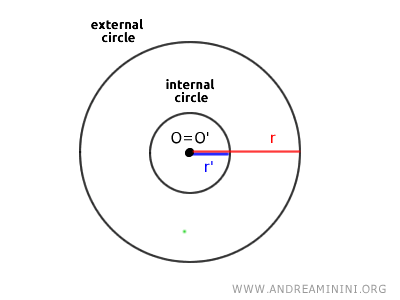
The circles are coincident circles if they have the same center \( O = O' \) and the same radius \( r = r' \).
A Practical Example
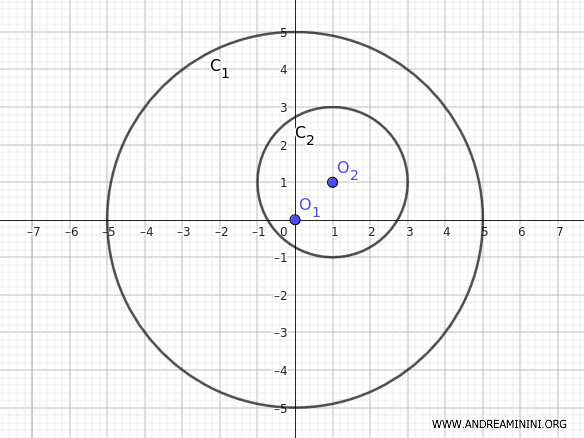
Let's consider two circles.
- The first circle \( C_1 \) has its center at \( O_1 = (0, 0) \) and a radius of \( r_1 = 5 \) cm.
- The second circle \( C_2 \) has its center at \( O_2 = (1, 1) \) and a radius of \( r_2 = 2 \) cm.
We calculate the distance between the centers \( O_1 \) and \( O_2 \) using the Euclidean distance formula.
$$ d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$
In this case, \( O_1 = (0, 0) \) and \( O_2 = (1, 1) \), so \( x_1 = 0 \), \( y_1 = 0 \), \( x_2 = 1 \), and \( y_2 = 1 \)
$$ d = \sqrt{(1 - 0)^2 + (1 - 0)^2} $$
$$ d = \sqrt{1 + 1} $$
$$ d = \sqrt{2} \approx 1.41 \text{ cm} $$
Next, we check if one circle is inside the other.
A circle is inside another if the distance between the centers is less than the absolute difference of their radii:
$$ d < | r_1 - r_2 | $$
The distance between the centers is approximately \( d = 1.41 \) cm, while the radii are \( r_1 = 5 \) cm and \( r_2 = 2 \) cm.
$$ 1.41 < 5 - 2 $$
$$ 1.41 < 3 $$
Therefore, the circle with the smaller radius \( C_2 \) is inside the larger circle \( C_1 \).
Internal Circles in Analytic Geometry
To determine if one circle is inside another using their equations, we need to identify and compare their radii and the positions of their centers.
Suppose we have two circles with the following equations:
$$ C_1: x^2 + y^2 + a_1x + b_1y + c_1 = 0 $$
$$ C_2: x^2 + y^2 + a_2x + b_2y + c_2 = 0 $$
First, we find the centers and radii of the two circles.
Note: To find these, we can directly use the formulas for the center of a circle $$ \left(-\frac{a}{2}, -\frac{b}{2}\right) $$ and for the radius $$ r = \sqrt{\left(\frac{a}{2}\right)^2 + \left(\frac{b}{2}\right)^2 - c} $$. However, I prefer to go through all the steps, as the general procedure allows solving the problem even if the center and radius formulas are not remembered.
To find the centers of the circles, we rewrite the equations in standard form:
$$ (x-h)^2 + (y-k)^2 = r^2 $$
Where \((h, k)\) is the center and \(r\) is the radius.
1] The First Circle in Standard Form
For the first circle \( x^2 + y^2 + a_1x + b_1y + c_1 = 0 \):
\[ x^2 + a_1x + y^2 + b_1y = -c_1 \]
Complete the square for the \( x \) and \( y \) terms:
\[ x^2 + a_1x + \left(\frac{a_1}{2}\right)^2 + y^2 + b_1y + \left(\frac{b_1}{2}\right)^2 = -c_1 + \left(\frac{a_1}{2}\right)^2 + \left(\frac{b_1}{2}\right)^2 \]
Thus, we get the equation in standard form:
\[ \left(x + \frac{a_1}{2}\right)^2 + \left(y + \frac{b_1}{2}\right)^2 = \left(\frac{a_1}{2}\right)^2 + \left(\frac{b_1}{2}\right)^2 - c_1 \]
In this form, it’s easy to identify the center coordinates and the radius:
- The center of the first circle is $$ \left(-\frac{a_1}{2}, -\frac{b_1}{2}\right) $$
- The radius of the first circle is $$ r_1 = \sqrt{\left(\frac{a_1}{2}\right)^2 + \left(\frac{b_1}{2}\right)^2 - c_1} $$
2] The Second Circle in Standard Form
Similarly, we perform the same calculations for the second circle:
$$ x^2 + y^2 + a_2x + b_2y + c_2 = 0 $$
$$ x^2 + y^2 + a_2x + b_2y = -c_2 $$
Complete the square for the \( x \) and \( y \) terms:
\[ x^2 + a_2x + \left(\frac{a_2}{2}\right)^2 + y^2 + b_2y + \left(\frac{b_2}{2}\right)^2 = -c_2 + \left(\frac{a_2}{2}\right)^2 + \left(\frac{b_2}{2}\right)^2 \]
And we get the second circle's equation in standard form:
\[ \left(x + \frac{a_2}{2}\right)^2 + \left(y + \frac{b_2}{2}\right)^2 = \left(\frac{a_2}{2}\right)^2 + \left(\frac{b_2}{2}\right)^2 - c_2 \]
From this, we can easily find the center and radius:
- The center of the second circle is $$ \left(-\frac{a_2}{2}, -\frac{b_2}{2}\right) $$
- The radius of the second circle is $$ r_2 = \sqrt{\left(\frac{a_2}{2}\right)^2 + \left(\frac{b_2}{2}\right)^2 - c_2} $$
3] Comparing the Distance Between Centers with the Difference in Radii
Now that we know the centers and radii, we can check if one circle is inside the other.
Calculate the distance between the centers of the two circles:
\[ d = \sqrt{\left(-\frac{a_1}{2} + \frac{a_2}{2}\right)^2 + \left(-\frac{b_1}{2} + \frac{b_2}{2}\right)^2} \]
Finally, compare the sum of the radii with the distance between the centers:
- If \( d + r_1 \leq r_2 \), then the first circle is inside the second.
- If \( d + r_2 \leq r_1 \), then the second circle is inside the first.
Alternatively, compare the absolute difference of the radii:
- If \( d \leq | r_1 - r_2 | \) and $ r_1 < r_2 $, then the first circle is inside the second.
- If \( d \leq | r_1 - r_2 | \) and $ r_1 > r_2 $, then the second circle is inside the first.
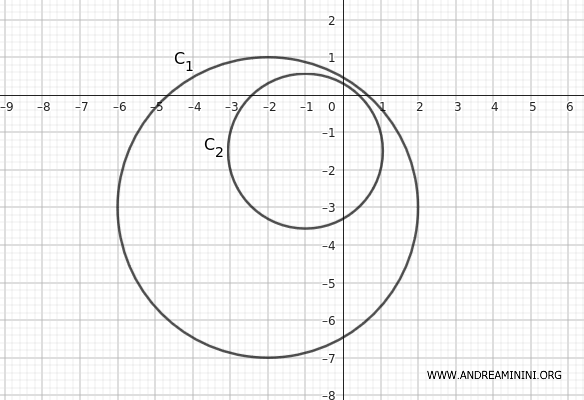
Example
Consider the circles with the following equations:
$$ C_1: x^2 + y^2 + 4x + 6y - 3 = 0 $$
$$ C_2: x^2 + y^2 + 2x + 3y - 1 = 0 $$
Complete the square to transform the circles into standard form.
For \( C_1: x^2 + y^2 + 4x + 6y - 3 = 0 \):
$$ x^2 + 4x + y^2 + 6y = 3 $$
$$ (x^2 + 4x + 4) + (y^2 + 6y + 9) = 3 + 4 + 9 $$
$$ (x + 2)^2 + (y + 3)^2 = 16 $$
In standard form, it’s easy to see the center of circle \( C_1 \) is $$ (-2, -3) $$
The radius is $$ r_1 = \sqrt{16} = 4 $$
Explanation: To complete the square for $ x^2 + 4x $, add $ +4 $ to both sides of the equation. This gives $ x^2 + 4x + 4 = (x+2)^2 $. Similarly, to complete the square for $ y^2 + 6y $, add $ +9 $ to both sides of the equation. This gives $ y^2 + 6y + 9 = (y+3)^2 $.
For \( C_2: x^2 + y^2 + 2x + 3y - 1 = 0 \):
$$ x^2 + 2x + y^2 + 3y = 1 $$
$$ (x^2 + 2x + 1) + (y^2 + 3y + \frac{9}{4}) = 1 + 1 + \frac{9}{4} $$
$$ (x + 1)^2 + \left(y + \frac{3}{2}\right)^2 = \frac{17}{4} $$
So, the center of \( C_2 \) is $$ (-1, -\frac{3}{2}) $$
The radius is:
$$ r_2 = \sqrt{\frac{17}{4}} = \frac{\sqrt{17}}{2} \approx 2.06 $$
With the centers at \((-2, -3)\) and \((-1, -\frac{3}{2})\) and the radii \( r_1 = 4 \) and \( r_2 = 2.06 \), we can calculate the distance between the centers and compare it to the absolute difference of the radii:
$$ d < | r_1 - r_2 | $$
The distance (d) between the centers \((-2, -3)\) and \((-1, -\frac{3}{2})\) is:
$$ d = \sqrt{(x_1 + x_2)^2 + (y_1 + y_2)^2} $$
$$ d = \sqrt{(-2 + 1)^2 + \left(-3 + \frac{3}{2}\right)^2} $$
$$ d = \sqrt{(-1)^2 + \left(-\frac{3}{2}\right)^2} $$
$$ d = \sqrt{1 + \frac{9}{4}} $$
$$ d = \sqrt{\frac{4}{4} + \frac{9}{4}} $$
$$ d = \sqrt{\frac{13}{4}} $$
$$ d = \frac{\sqrt{13}}{2} \approx 1.8 $$
Then, we check if one circle is inside the other.
Compare the absolute difference of the radii and the distance between the centers:
$$ d < | r_1 - r_2 | $$
$$ 1.8 < | 4 - 2.06 | $$
$$ 1.8 < 1.94 $$
This confirms that one circle is inside the other.
Since \( r_2 < r_1 \), we can conclude that the second circle \( C_2 \) is inside the first circle \( C_1 \).
Therefore, \( C_2 \) is inside \( C_1 \).
Concentric Circles in Analytic Geometry
Two concentric circles have the same center but different radii. In analytic geometry, this means the equations of the two circles will have the same coefficients $ a=a' $ and $ b=b' $ for the \( x \) and \( y \) terms, but different values for the constant term $ c \ne c' $.
Consider the general equations of the two circles:
$$ C_1 : x^2 + y^2 + ax + by + c = 0 $$
$$ C_2: x^2 + y^2 + a'x + b'y + c' = 0 $$
If the two circles are concentric, they have the same center.
This means the terms involving \( x \) and \( y \) (i.e., \( ax=a'x \) and \( by=b'y \)) must be identical in both equations.
Thus, the coefficients \( a \) and \( b \) must be equal:
$$ a = a' $$
$$ b = b' $$
The only difference between two concentric circles is the constant term \( c \), representing the difference in the radii of the circles. Therefore, \( c \neq c' \).
$$ c \neq c' $$
Note: When the equations of the two circles have the same coefficients $ a=a' $, $ b=b' $, and $ c=c' $, then the two circles have the same center and radius, meaning they are coincident circles.
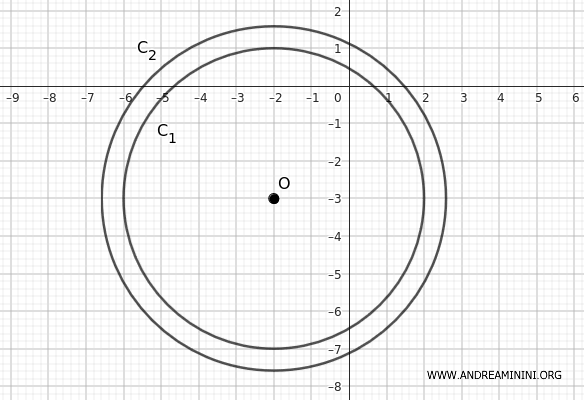
Practical Example
In this exercise, consider the following circles:
$$ C_1 : x^2 + y^2 + 4x + 6y - 3 = 0 $$
$$ C_2: x^2 + y^2 + 4x + 6y - 8 = 0 $$
The centers of the circles are both \( \left(-2, -3\right) \) because the coefficients of \( x \) and \( y \) are the same.
$$ (x_0, y_0) = ( - \frac{a}{2} , -\frac{b}{2} ) = ( - \frac{4}{2} , -\frac{6}{2} ) = (-2, -3) $$
Knowing that the formula for calculating the radius of a circle is:
$$ r = \sqrt{\left(\frac{a}{2}\right)^2 + \left(\frac{b}{2}\right)^2 - c} $$
The radii of the two circles are:
- For the first circle: $$ r_1 = \sqrt{(-2)^2 + (-3)^2 + 3} = \sqrt{4 + 9 + 3} = \sqrt{16} = 4 $$
- For the second circle: $$ r_2 = \sqrt{(-2)^2 + (-3)^2 + 8} = \sqrt{4 + 9 + 8} = \sqrt{21} \approx 4.58 $$
The distance between the centers is zero \( d=0 \) because they are concentric, and the radii are different, so the two circles are not coincident.
$$ d < | r_1 - r_2 | $$
$$ 0 < | 4 - 4.58 | $$
$$ 0 < 0.58 $$
This confirms that one circle is inside the other.
Comparing the radii \( r_1 = 4 \) and \( r_2 \approx 4.58 \), we deduce that the first circle $ C_1 $, which has the smaller radius (radius 4), is inside the second circle $ C_2 $ (radius approximately 4.58).
And so on.
