Pi
Pi is an irrational number that represents the ratio of any circle's circumference (C) to its diameter (d). Its approximate value is $$ \pi = \frac{C}{d} = 3.1415926535 $$
Since π (pi) is irrational, it cannot be expressed as an exact fraction and its decimal representation is infinite and non-repeating.
The Greek letter π is used because it's the first letter of the word "perimeter." With this value, one can determine the circumference of a circle C=2πr, or the circle's perimeter.
$$ C = \pi \cdot d = \pi \cdot 2r $$
Where r is the radius of the circle and is always equal to half the diameter d=2r.
The Greek mathematician Archimedes was the first to compute the value of pi with precision up to two decimal places, using polygons with 96 sides for reference.
The History of Pi
The origins of the number 3.14, better known as Pi (π), date back to the earliest civilizations in history, deeply rooted in ancient geometry.
It was quickly discovered that the ratio between a circle's circumference and its diameter is a constant number.
In other words, no matter the size of a circle, dividing its circumference by the diameter always yields approximately the value of π, which is about 3.14.
The earliest approximations trace back to the Babylonians and Egyptians.
The Babylonians used an approximate value of 3 1/8 (3.125) for π, while an Egyptian estimate found in the Rhind Papyrus suggests a value of about 3.16.
These early estimates were remarkably close to the true value of π, considering the primitive methods available for measurement and calculation.
However, it was the ancient Greeks who refined the calculation, thanks to mathematicians like Archimedes.
Archimedes of Syracuse, who lived in the 3rd century BC, brought the calculation of π to a high level of precision using a clever geometric method known today as the method of exhaustion.
He used regular inscribed and circumscribed polygons to approximate the circumference of a circle.
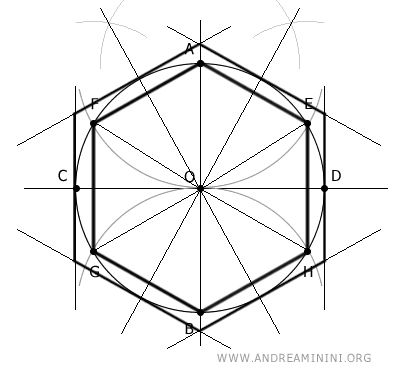
Specifically, he started with hexagons and doubled the number of sides of the polygons repeatedly until he reached a polygon with an impressive 96 sides!
This method allowed Archimedes to determine that the value of π was between 3 1/7 (about 3.1429) and 3 10/71 (about 3.1408), an astonishingly accurate approximation for that time.
Today, we know this mathematical constant by the letter "pi" (π).
In fact, this naming is much more recent. It was introduced much later, in 1706, by Welsh mathematician William Jones and Swiss mathematician Leonhard Euler in the 18th century.
Note. With the advent of computers, the number π has been calculated with precision to millions of decimal places. It's a mathematical challenge that continues today and is often used to test the limits of computer numerical computation and number theory.
Calculating Pi
The quest for pi starts with the need to calculate a circle's perimeter, i.e., finding the length of the circumference.
The circumference of a circle is C=2πr
I construct a regular hexagon inscribed in the circle.
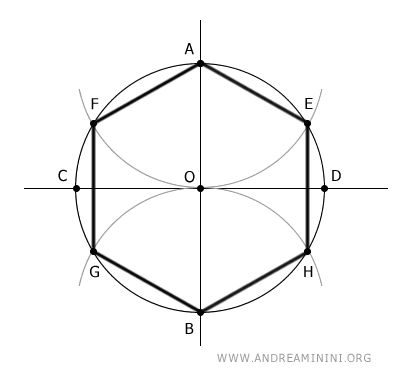
Note. To draw an inscribed hexagon, simply draw the perpendicular axes and sketch two arcs with the same radius as the circle.
The distance between the center of the circle (O) and any vertex of the inscribed hexagon is equal to the radius.
$$ \overline{OA} = \overline{OB} = ... = r $$
Since the hexagon has six sides and the sum of the internal angles of a circle is 360°, the central angle ∠AOE corresponding to one-sixth of the circumference is 360°/6=60°.
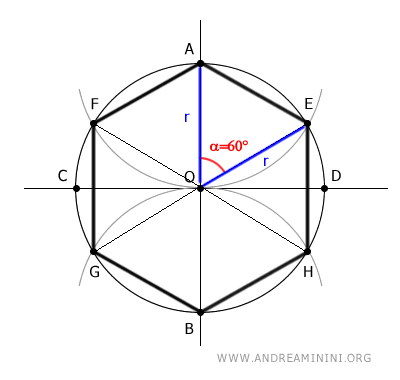
The triangle OAE is an isosceles triangle because it has two congruent sides OA≅OE, as they are both equal to the radius r of the circle OA=r and OE=r.
Knowing that in an isosceles triangle the base angles are congruent, I deduce that the angles β≅γ of the triangle OAE are congruent.
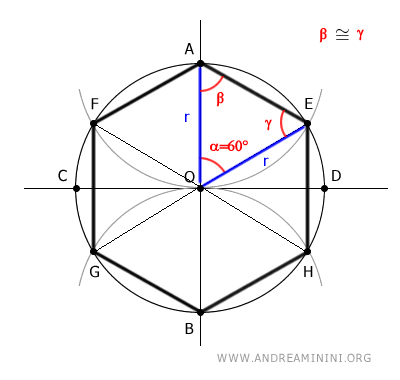
Knowing that one angle of the triangle OAE is 60° and the sum of the internal angles of a triangle is always equal to 180°, I deduce that the sum of the remaining angles is equal to 120°
$$ 180° - \alpha = \beta + \gamma $$
$$ 180° - 60° = \beta + \gamma $$
$$ 120° = \beta + \gamma $$
Since the angles β≅γ are congruent, I deduce that each of them is equal to 60°
$$ \beta = \gamma = 60° $$
The triangle OAE has all congruent angles β≅γ≅α≅60°.
Therefore, the triangle OAE is also an equilateral triangle, meaning all its sides are congruent.
$$ \overline{OA} \cong \overline{OE} \cong \overline{AE} $$
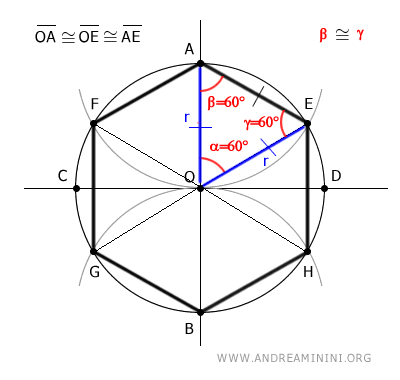
Knowing that OA=OE=r are equal to the radius, I deduce that the side of the hexagon AE=r is also equal to the radius of the circle.
$$ \overline{AE} = r $$
Thus, in a regular hexagon inscribed in a circle, the perimeter (P) of the hexagon is equal to six times the radius of the circle.
$$ P = 6r $$
Being an inscribed hexagon, its perimeter is less than that of the circle.
$$ 6 r < 2 \pi r $$
I simplify by dividing both sides of the inequality by two
$$ 3 r < \pi r $$
Then divide by r on both sides
$$ 3 < \pi $$
Thus, I deduce that the value of pi is greater than 3.
Next, I construct a regular hexagon circumscribed around the circle.
To do this, I draw lines passing through the center and the midpoints of the six equilateral triangles that make up the inscribed hexagon in the circle.
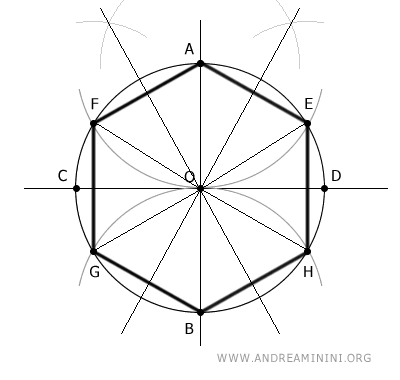
Then I draw tangent lines to the circle that intersect the lines passing through the midpoints.
Simply draw a perpendicular line to the previous lines at the various midpoints.
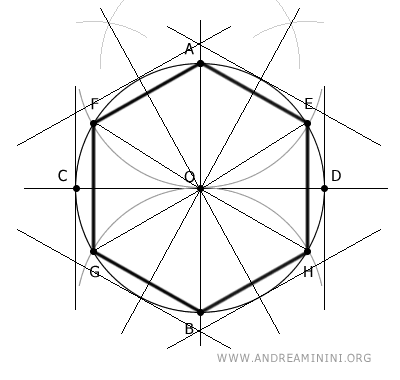
The final result is a circumscribed hexagon.
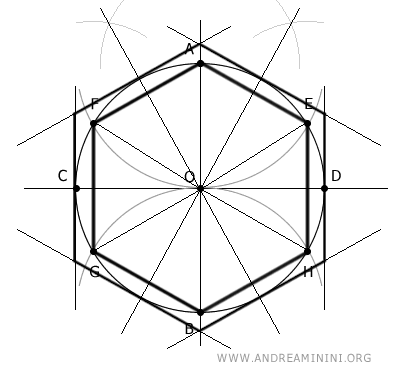
To continue the study with greater clarity, I present the drawing with only the circumscribed hexagon.
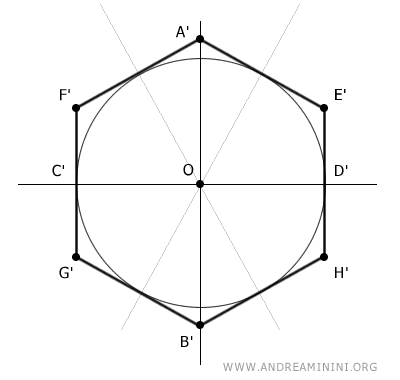
I draw segments from the origin to the vertices of the hexagon A', B', E', F', G', H'.
In this way, I divide the hexagon into six congruent triangles.
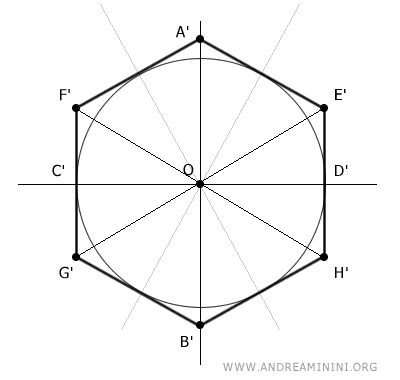
I consider the triangle OE'H'.
Again, the hexagon has six sides and the sum of the internal angles of a circle is 360°, so the central angle ∠E'OH' corresponding to one-sixth of the circumference is 360°/6=60°.
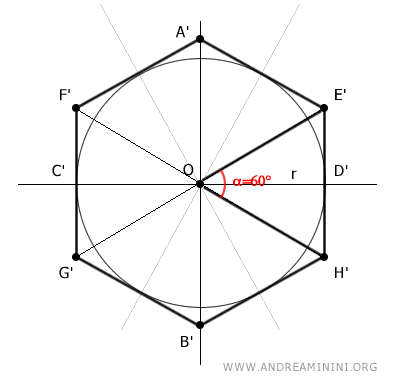
In this case, the radius of the circle coincides with the segment OD', which is the height of the triangle OE'H',
The triangle OE'H' consists of two right-angle triangles OE'D' and OH'D' with angles equal to 30°, 60°, 90°
Therefore, I can calculate the length of the legs E'D' and H'D' using the formula for a right-angle triangle with acute angles of 30° and 60°
$$ \overline{E'D'} = \frac{ \overline{OD'} \sqrt{3} }{3} $$
$$ \overline{H'D'} = \frac{ \overline{OD'} \sqrt{3} }{3} $$
Therefore, knowing that the side E'H'=E'D'+H'D', I obtain:
$$ \overline{E'H'} = 2 \cdot \frac{ \overline{OD'} \sqrt{3} }{3} $$
The segment OD' is the radius of the circle (r)
$$ \overline{E'H'} = 2 \cdot \frac{ r \cdot \sqrt{3} }{3} $$
Having obtained the length of the hexagon's side based on the radius, I calculate the perimeter of the regular hexagon.
The perimeter P of the regular hexagon is equal to six times the side E'H'
$$ P = 6 \cdot \overline{E'H'} $$
$$ P = 6 \cdot 2 \cdot \frac{ r \cdot \sqrt{3} }{3} $$
$$ P = 12 \cdot \frac{ r \cdot \sqrt{3} }{3} $$
$$ P = 4 \cdot r \cdot \sqrt{3} $$
Being a hexagon circumscribed around the circle, its perimeter is greater than the circle's circumference C=2πr
$$ P > C $$
$$ 4 \cdot r \cdot \sqrt{3} > 2 \pi \cdot r $$
Now I simplify by dividing both sides of the inequality by r
$$ 4 \cdot \ sqrt{3} > 2 \pi $$
Then I derive pi by dividing both sides by 2
$$ 2 \cdot \sqrt{3} > \pi $$
The product 2√3 is approximately 3.46.
$$ 3.46 > \pi $$
Therefore, the value of pi is less than 3.46.
In conclusion, thanks to the perimeter of the inscribed and circumscribed hexagons, it is understood that the value of pi is greater than 3 and less than 3.46.
Note. This demonstrates that the length of the circumference is the element that separates the class of perimeters of regular inscribed polygons from that of regular circumscribed polygons around the circle.
By repeating the same operation using polygons with more sides, the calculation becomes more precise.
It is worth noting that Archimedes managed to find the first two decimal places of the value of pi using a polygon with 96 sides.
Insights
Some thoughts and side notes on Pi.
- How to remember Pi?
Most people remember Pi as 3.14, but recalling the digits that follow is often a challenge. A common tactic for memorizing these digits involves using mnemonic devices. For instance, one approach is to craft a sentence or a rhyme where the number of letters in each word represents a digit of Pi. For example, a mnemonic in English could be: "May I have a large container of coffee, cream, and sugar?"

And so on.
